An Algorithm for Modified Nodal Analysis

This document describes an algorithmic method for generating MNA (Modified Nodal Analysis) equations for systems with only resistors and idependent sources.. It consists of several parts:.

Many of the ideas and notation from this page are from Litovski, though the discussion here is quite simpler because only independent voltage and current sources are considered.

Review

Recall from the previous document:

MNA applied to a circuit with only passive elements (resistors) and independent current and voltage sources results in a matrix equation of the form:

\[{\mathbf{Ax = z}}\]

For a circuit with n nodes and m independent voltage sources:

The A matrix:
- is (n+m)x(n+m) in size, and consists only of known quantities.
- the nxn part of the matrix in the upper left:
  - has only passive elements
  - elements connected to ground appear only on the diagonal
  - elements not connected to ground are both on the diagonal and off-diagonal terms.
- the rest of the A matrix (not included in the nxn upper left part) contains only 1, -1 and 0 (other values are possible if there are dependent current and voltage sources; I have not considered these cases. Consult Litovski if interested.)
The x matrix:
- is an (n+m)x1 vector that holds the unknown quantities (node voltages and the currents through the independent voltage sources).
- the top n elements are the n node voltages.
- the bottom m elements represent the currents through the m independent voltage sources in the circuit.
The z matrix:
- is an (n+m)x1 vector that holds only known quantities
- the top n elements are either zero or the sum and difference of independent current sources in the circuit.
- the bottom m elements represent the m independent voltage sources in the circuit.

The circuit is solved by a simple matrix manipulation:

\[{\mathbf{x = }}{{\mathbf{A}}^{ - 1}}{\mathbf{z}}\]

Though this may be difficult by hand, it is straightforward and so is easily done by computer.

Notational Convention

Obviously, the notation used does not change the solution. However the convention described below will make it quite easy to develop the matrices necessary for solution of the circuit.

Ground is labeled as node 0.
The other nodes are labeled consecutively from 1 to n.
We will refer to the voltage at node 1 as v_1, at node 2 as v_2 and so on.
The naming of the independent voltage sources is quite loose, but the names must start with the letter "V" and must be unique from any node names. For our purposes we will require that independent voltage sources have no underscore ("_") in their names. So the names Va, Vsource, V1, Vxyz123 are all legitimate names, but V_3, V_A, Vsource_1 are not.
The current through a voltage source will be labeled with "I_" followed by the name of the voltage source. Therefore the current through Va is I_Va, the current through VSource is I_VSource, etc...
The naming of the independent current sources is similar; the names must start with the letter "I" and must have no underscore ("_") in their names. So the names Ia, Isource, I1, Ixyz123 are all legitimate names, but I_3, I_A, Isource_1 are not.
Note: some of these rules are arbitrary (particularly the naming conventions) but will make development of a MATLAB based algorithm easier.

These rules are somewhat restrictive (more so than they need to be) but they make development of the algorithm easier while still allowing quite a bit of freedom.

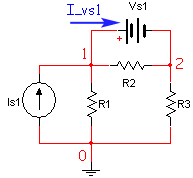
These rules are easily explained with an example (Example 3 from previous page):

This circuit is labeled according to the guidelines above. Ground is node 0 and the other two nodes are labeled 1 and 2. The voltage and current sources have labels with no underscores and the current through the voltage source Vs1 is labeled I_Vs1. We will discuss how to use this diagram (with these labels) to generate the MNA equations below.

Generating the MNA matrices

There are three matrices we need to generate, the A matrix, the x matrix and the z matrix. Each of these will be created by combining several individual sub-matrices. To motivate the rules for generating the matrices we will consider the two sample circuits below (example 2 and example 3 from previous web page, with Notational Convention as above). I simply state the resulting MNA equations, but in the following text we will show how to generate each one.

Case 1

Circuit Diagram

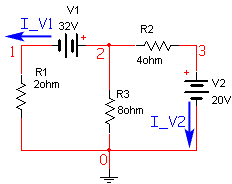Case 2

Circuit Diagram

The A matrix

The A matrix will be developed as the combination of 4 smaller matrices, G, B, C, and D.

\[{\mathbf{A}} = \left[ {\begin{array}{*{20}{c}} {\mathbf{G}}&{\mathbf{B}} \\ {\mathbf{C}}&{\mathbf{D}} \end{array}} \right]\]

The A matrix is (m+n)×(m+n) (n is the number of nodes, and m is the number of independent voltage sources) and:

the G matrix is n×n and is determined by the interconnections between the passive circuit elements (resistors)
the B matrix is n×m and is determined by the connection of the voltage sources.
the C matrix is m×n and is determined by the connection of the voltage sources. ( B and C are closely related, particularly when only independent sources are considered).
the D matrix is m×m and is zero if only independent sources are considered.

Rules for making the G matrix

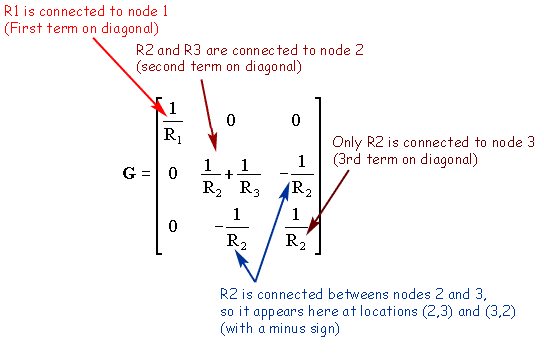
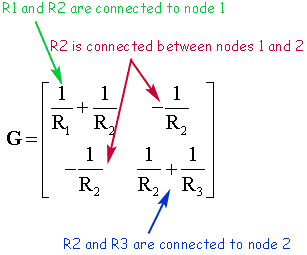
The G matrix is an n×n matrix formed in two steps

Each element in the diagonal matrix is equal to the sum of the conductance (one over the resistance) of each element connected to the corresponding node. So the first diagonal element is the sum of conductances connected to node 1, the second diagonal element is the sum of conductances connected to node 2, and so on.
The off diagonal elements are the negative conductance of the element connected to the pair of corresponding node. Therefore a resistor between nodes 1 and 2 goes into the G matrix at location (1,2) and locations (2,1).

Demonstrations

Case 1
Circuit Diagram	MNA Equations
	\[{\mathbf{G}} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{R_1}}}}&0&0 \\ 0&{\frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}}&{ - \frac{1}{{{R_2}}}} \\ 0&{ - \frac{1}{{{R_2}}}}&{\frac{1}{{{R_2}}}} \end{array}} \right]\]

Case 2
Circuit Diagram	MNA Equations
	\[{\mathbf{G}} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}}&{ - \frac{1}{{{R_2}}}} \\ { - \frac{1}{{{R_2}}}}&{\frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}} \end{array}} \right]\]

If an element is grounded, it will only have contribute to one entry in the G matrix -- at the appropriate location on the diagonal. If it is ungrounded it will contribute to four entries in the matrix -- two diagonal entries (corresponding to the two nodes) and two off-diagonal entries.

Rules for making the B matrix

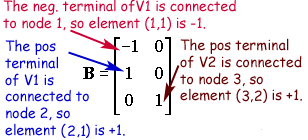
The B matrix is an n×m matrix with only 0, 1 and -1 elements. Each location in the matrix corresponds to a particular voltage source (first dimension) or a node (second dimension). If the positive terminal of the ith voltage source is connected to node k, then the element (i,k) in the B matrix is a 1. If the negative terminal of the ith voltage source is connected to node k, then the element (i,k) in the B matrix is a -1. Otherwise, elements of the B matrix are zero.

Demonstrations

Case 1
Circuit Diagram	MNA Equations
	\[{\mathbf{B}} = \left[ {\begin{array}{*{20}{c}} { - 1}&0 \\ 1&0 \\ 0&1 \end{array}} \right]\]

Case 2
Circuit Diagram	MNA Equations
	\[{\mathbf{B}} = \left[ {\begin{array}{*{20}{c}} 1 \\ { - 1} \end{array}} \right]\]

If a voltage source is ungrounded, it will have two elements in the B matrix (a 1 and a -1 in the same column). If it is grounded it will only have one element in the matrix.

Rules for making the C matrix

The C matrix is an m×n matrix with only 0, 1 and -1 elements. Each location in the matrix corresponds to a particular node (first dimension) or voltage source (second dimension). If the positive terminal of the ith voltage source is connected to node k, then the element (k,i) in the C matrix is a 1. If the negative terminal of the ith voltage source is connected to node k, then the element (k,i) in the C matrix is a -1. Otherwise, elements of the C matrix are zero.

In other words, the C matrix is the transpose of the B matrix. (This is not the case when dependent sources are present.)

Case 1: ${\mathbf{C}} = \left[ {\begin{array}{*{20}{c}} { - 1}&1&0 \\ 0&0&1 \end{array}} \right]$

Case 2: ${\mathbf{C}} = \left[ {\begin{array}{*{20}{c}} 1&{ - 1} \end{array}} \right]$

Rules for making the D matrix

The D matrix is an m×m matrix that is composed entirely of zeros. (It can be non-zero if dependent sources are considered.)

Case 1: ${\mathbf{D}} = \left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&0 \end{array}} \right]$

Case 2: ${\mathbf{D}} = \left[ 0 \right]$

The x matrix

The x matrix holds our unknown quantities and will be developed as the combination of 2 smaller matrices v and j. It is considerably easier to define than the A matrix.

\[{\mathbf{x}} = \left[ {\begin{array}{*{20}{c}} {\mathbf{v}} \\ {\mathbf{j}} \end{array}} \right]\]

The x matrix is (m+n)×1 (n is the number of nodes, and m is the number of independent voltage sources) and:

the v matrix is n×1 and hold the unknown voltages
the j matrix is m×1 and holds the unknown currents through the voltage sources

Rules for making the v matrix

The v matrix is an n×1 matrix formed of the node voltages. Each element in v corresponds to the voltage at the equivalent node in the circuit (there is no entry for ground -- node 0).

For example if a circuit has three nodes, the v matrix is

\[{\mathbf{v}} = \left[ {\begin{array}{*{20}{c}} {v\_1} \\ {v\_2} \\ {v\_3} \end{array}} \right]\]

For a circuit with n nodes we get

\[{\mathbf{v}} = = \left[ {\begin{array}{*{20}{c}} {v\_1} \\ \vdots \\ {v\_n} \end{array}} \right]\]

and so on.

Rules for making the j matrix

The j matrix is an m×1 matrix, with one entry for the current through each voltage source. So if there are two voltage sources V1 and V2, the j matrix will be:

\[{\mathbf{j}} = \left[ {\begin{array}{*{20}{c}} {i\_V1} \\ {i\_V2} \end{array}} \right]\]

Demonstrations for the x matrix.

Case 1
Circuit Diagram	MNA Equations
	\[{\mathbf{v}} = \left[ {\begin{array}{{20}{c}} {v\_1} \\ {v\_2} \\ {v\_3} \end{array}} \right],\;{\mathbf{j}} = \left[ {\begin{array}{{20}{c}} {i\_V1} \\ {i\_V2} \end{array}} \right],\quad {\mathbf{x}} = \left[ {\begin{array}{{20}{c}} {\mathbf{v}} \\ {\mathbf{j}} \end{array}} \right] = \left[ {\begin{array}{{20}{c}} {\begin{array}{{20}{c}} {v\_1} \\ {v\_2} \\ {v\_3} \end{array}} \\ {\begin{array}{{20}{c}} {i\_V1} \\ {i\_V2} \end{array}} \end{array}} \right]\]

Case 2
Circuit Diagram	MNA Equations
	\[{\mathbf{v}} = \left[ {\begin{array}{{20}{c}} {v\_1} \\ {v\_2} \end{array}} \right],\;{\mathbf{j}} = \left[ {i\_Vs1} \right],\quad {\mathbf{x}} = \left[ {\begin{array}{{20}{c}} {\mathbf{v}} \\ {\mathbf{j}} \end{array}} \right] = \left[ {\begin{array}{{20}{c}} {\begin{array}{{20}{c}} {v\_1} \\ {v\_2} \end{array}} \\ {i\_Vs1} \end{array}} \right]\]

The z matrix

The z matrix holds our independent voltage and current sources and will be developed as the combination of 2 smaller matrices i and e. It is quite easy to formulate.

\[{\mathbf{z = }}\left[ {\begin{array}{*{20}{c}} {\mathbf{i}} \\ {\mathbf{e}} \end{array}} \right]\]

The z matrix is (m+n)×1 (n is the number of nodes, and m is the number of independent voltage sources) and:

the i matrix is n×1 and contains the sum of the currents through the passive elements into the corresponding node (either zero, or the sum of independent current sources).
the e matrix is m×1 and holds the values of the independent voltage sources.

Rules for making the i matrix

The i matrix is an n×1 matrix with each element of the matrix corresponding to a particular node. The value of each element of i is determined by the sum of current sources into the corresponding node. If there are no current sources connected to the node, the value is zero.

Rules for making the e matrix

The e matrix is an m×1 matrix with each element of the matrix equal in value to the corresponding independent voltage source.

Demonstrations for the z matrix.

Case 1
Circuit Diagram	MNA Equations
	\[{\mathbf{i}} = \left[ {\begin{array}{{20}{c}} 0 \\ 0 \\ 0 \end{array}} \right],\;{\mathbf{e}} = \left[ {\begin{array}{{20}{c}} {V1} \\ {V2} \end{array}} \right],\quad {\mathbf{z}} = \left[ {\begin{array}{{20}{c}} {\begin{array}{{20}{c}} 0 \\ 0 \\ 0 \end{array}} \\ {\begin{array}{*{20}{c}} {V1} \\ {V2} \end{array}} \end{array}} \right]\]

Case 2
Circuit Diagram	MNA Equations
	\[{\mathbf{i}} = \left[ {\begin{array}{{20}{c}} {Is1} \\ 0 \end{array}} \right],\;{\mathbf{e}} = \left[ {Vs1} \right],\quad {\mathbf{z}} = \left[ {\begin{array}{{20}{c}} {\begin{array}{*{20}{c}} {Is1} \\ 0 \end{array}} \\ {Vs1} \end{array}} \right]\]

Putting it Together

We can now write out the full matrix solutions for both cases that we have been developing.

Case 1
Circuit Diagram	MNA Equations
	\[\left[ {\begin{array}{{20}{c}} {\frac{1}{{{R_1}}}}&0&0&{ - 1}&0 \\ 0&{\frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}}&{ - \frac{1}{{{R_2}}}}&1&0 \\ 0&{ - \frac{1}{{{R_2}}}}&{\frac{1}{{{R_2}}}}&0&1 \\ { - 1}&1&0&0&0 \\ 0&0&1&0&0 \end{array}} \right]\left[ {\begin{array}{{20}{c}} {\begin{array}{{20}{c}} {v\_1} \\ {v\_2} \\ {v\_3} \end{array}} \\ {\begin{array}{{20}{c}} {i\_V1} \\ {i\_V2} \end{array}} \end{array}} \right] = \left[ {\begin{array}{{20}{c}} {\begin{array}{{20}{c}} 0 \\ 0 \\ 0 \end{array}} \\ {\begin{array}{*{20}{c}} {V1} \\ {V2} \end{array}} \end{array}} \right]\]

Case 2
Circuit Diagram	MNA Equations
	\[\left[ {\begin{array}{{20}{c}} {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}}&{ - \frac{1}{{{R_2}}}}&1 \\ { - \frac{1}{{{R_2}}}}&{\frac{1}{{{R_2}}} + \frac{1}{{{R_3}}}}&{ - 1} \\ 1&{ - 1}&0 \end{array}} \right]\left[ {\begin{array}{{20}{c}} {\begin{array}{{20}{c}} {v\_1} \\ {v\_2} \end{array}} \\ {i\_Vs1} \end{array}} \right] = \left[ {\begin{array}{{20}{c}} {\begin{array}{*{20}{c}} {Is1} \\ 0 \end{array}} \\ {Vs1} \end{array}} \right]\]

If you are still unsure about the application of the algorithm, some more examples are available.

So far we have only dealt with resistors and independent voltage and current sources. The next document will show that adding capacitors and inductors is trivial, and adding op-amps only adds minimally to the difficulty.

References

Replace