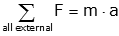
Developing Mathematical Models of Translating Mechanical Systems

Introduction

While the previous page (System Elements) introduced the fundamental elements of translating mechanical systems, as well as their mathematical models, no actual systems were discussed.  This page discusses how the system elements can be included in larger systems, and how a system model can be developed.   The actual solution of such models requires manipulation of the model into a useful form and is discussed elsewhere.

Contents

D'Alembert's Law

Newton's second law states that an object accelerates in the direction of an applied force, and that this acceleration is inversely proportional to the force, or

 

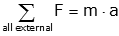
we will bring the right-hand side to the left and express this as

 

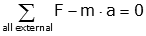
If we consider the m·a term to be a force, we are left with D'Alembert's law

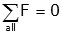
We will call the m·a term D'Alembert's force.  It is an inertial force that arises when you try to accelerate a mass.  To visualize this consider pushing against a mass (in the absence of friction) with your hand in the positive direction.  Your hand experiences a force in the direction opposite to that of the direction of the force (this is the -m·a term).   The inertial force is always in a direction opposite to the defined positive direction (see the first example below).

This formulation (the sum of forces at a point is equal to zero) also makes analogy to electrical systems easier (the sum of all currents into a node is zero); you needn't concern yourself with this now.

Key Concept: D'Alembert's Law

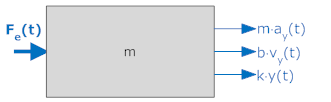
Equations of motion for translating mechanical system depend on the application of D'Alembert's law.  Using this principle we say that the sum of force on an object is equal to zero,

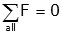
but we must also take the inertial force (m·a) as one of these forces.  This inertial force is in the opposite direction from the defined positive direction.

Free Body Diagrams

Introduction

We can apply D'Alembert's law to develop equations of motion for translating mechanical systems through the use of free body diagrams.  To do this we draw a free body diagram for each unknown position in a system.

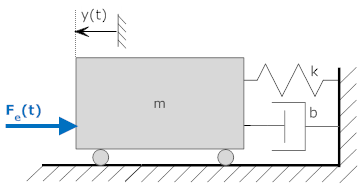
Example: Simple Mass-Spring-Dashpot system

Consider a simple system with a mass that is separated from a wall by a spring and a dashpot.  The mass could represent a car, with the spring and dashpot representing the car's bumper.  An external force is also shown.   Only horizontal motion and forces are considered.

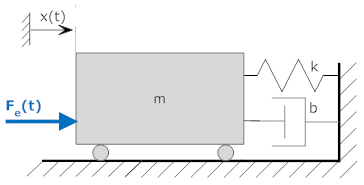
There is only one position in this system defined by the variable "x" that is positive to the right.  We assume that x=0 when the spring is in its relaxed state. 

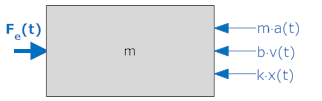
To develop a free body diagram we sum all the forces to zero.  There are four forces:

  1. An external force (Fe)
  2. A force from the spring.  To determine the direction consider that the position "x" is defined positive to the right.  If the mass moves in the positive "x" direction, the spring is compressed and exerts a force on the mass.  So there will be a force from the spring, k·x, to the left.
  3. A force from the dashpot.  By an argument similar to that for the spring there will be a force from the dashpot, b·v, to the left.   (The velocity, v, is the derivative of x with respect to time.)
  4. Finally, there is the inertal force which is defined to be opposed to the defined direction of motion.  This is represented by m·a to the left.   (The acceleration, a, is the second derivative of x with respect to time.)  Don't forget this force, it is easy to do so.

The completed free body diagram is shown below

 

We sum all of these forces to zero and get

 

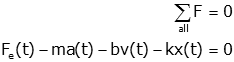
or

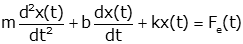
This equation is in our standard form that has system outputs (the unknown variables) on the left hand side and system inputs (the known variables) on the right hand side.  this is sometimes called input-output notation.

We will often use "dot" notation, using one dot above a variable to denote differentiation:

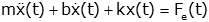
In addition, we will also make it implicit that certain variables are functions of time and omit the "(t)" in equations.  If we do so, the equations above become:

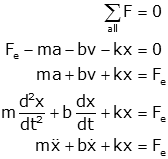
This is read as "m x double dot plus b x dot plus k x equals F sub e." 

Recall that the definition of the positive direction is arbitrary.  We could just as easilty have defined the positive direction to the left.  

Note: Differences between the text in this example and the one above are given as bold italics.

 

Now the free body diagram still has four forces,  but the reaction forces from the spring, friction and inertia have switched directions.

  1. An external force (Fe)
  2. A force from the spring.  To determine the direction consider that the position "y" is defined positive to the left.  If the mass moves in the positive "y" direction, the spring is stretched and exerts a force on the mass.  So there will be a force from the spring, k·y, to the right.
  3. A force from the dashpot.  By an argument similar to that for the spring there will be a force from the dashpot, b·vy, to the right.  (The velocity, vy, is the derivative of y with respect to time.)
  4. Finally, there is the inertal force which is defined to be opposed to the defined direction of motion.  This is represented by m·ay to the right.  (The acceleration, ay, is the second derivative of y with respect to time.)

Our equations become (with implicit functions of time):

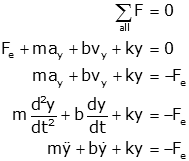
Note the changes of sign in the second equation and all those that follow.

 

Either set of equations (in terms of x or in terms of y) exactly, and identically, describes the behavior system.  In the first case a positive force (to the right) will cause the system to start moving in the positive x direction (to the right).  In the second case a positive force (to the right) will cause the system to start moving in the negative y direction (to the right).   The definition of positive directions is arbitrary with respect to the behavior of the system.

The example above was relatively simple, but this method applies to more complicated systems as well. 

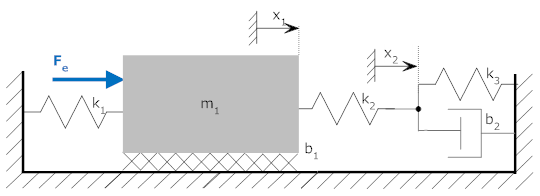
Example: More than one unknown position

 

The drawing above shows a system with two unknown positions, x1 and x2.  In this case we need to make two free body diagrams, one for x1, and one for x2.

Free body diagram at x1 Free body diagram at x2

There are 5 forces acting:

  1. The external force, Fe, to the right.
  2. The force due to k1.
    • If x1 increases, k1 elongates which causes a force at x1 to the left.
    • The resulting force is k1·x1 to the left.
  3. The force due to b1.
    • If x1 moves to the right  (i.e., the positive direction), the friction b1 causes a force (at x1) that is to the left.
    • The resulting force is b1·v1 to the left.
  4. The force due to k2.
    • If x1 increases, k2 compresses which causes a force at x1 to the left.
    • If x2 increases, k2 elongates which causes a force at x1 to the right.
    • The resulting force is k2·(x1-x2) to the left (or k2·(x2-x1) to the right)
  5. The force due to m1 (don't forget this - the inertial force!).
    • The resulting force is m1·a1 to the left (the inertial force is always in the opposite direction from the define positive direction).

There are 3 forces acting:

  1. The force due to k2.
    • If x1 increases (to the right), this compresses the spring and causes a force to the right at x2.
    • If x2 increases (to the right), this elongates the spring and causes a force pulling x2 to the left.
    • The resulting force is k2·(x1-x2) to the right (or k2·(x2-x1) to the left)
      (Note: this result is trivial because the torque on one end of k2 must be equal and opposite to the torque on the other end (calculated for the free body diagram for x1).)
  2. The force due to k3.
    • If x2 increases, this compresses the spring and causes a force to the left.
    • The resulting force is k3·x2 to the left.
  3. The force due to b2.
    • If x2 moves to the right (i.e., the positive direction), this compresses the dashpot and causes a force to the left.
    • The resulting force is b2·v2 to the left.

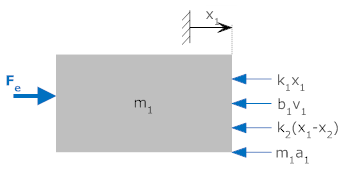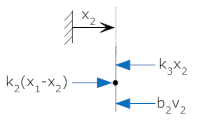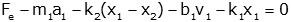We can put this in input-output form, and collect output variables: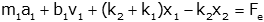

or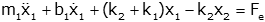

  
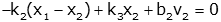Now collect terms and rewrite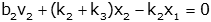

or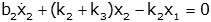

These equations represent a full mathematical model of the system.  It is possible to combine the two differential equations into a single equation and solve, but that topic is covered elsewhere.

Going Further:  To increase your understanding, and to underscore the fact that the choice of direction is arbitrary, this example is repeated with a different set of directions here.  You may wish to examine them side by side.  When choosing directions of motion the derivation of equations of motion is somewhat easier if all are chosen such that they have the same positive direction (e.g., all positive to the left or to the right).

Some notes about Free Body Diagrams:

You may have noticed some patterns in the directions of forces in free body diagrams.  Some of these are enumerated here:

  1. In the freebody diagrams, the directions corresponding to x1 and all of its derivatives are in the same direction and opposite the positive direction of x1.  This is true as long as their are no active elements (e.g., motors, amplifiers...) in the system. This is also true of x2; in the free body diagram for x2, the term k2(x1-x2) is to the right, but because of the negative sign the direction with respect to x2 is to the left as it is for k3x2 and b2v2.
  2. The force in k2 is equal and opposite on either end.  In the free body diagram for x1 (at the left side of spring k2) the arrow for k2(x1-x2) is to the left; the free body diagram for x2 (at the right side of spring k2) has the arrow going to the right.
  3. In all equations, the signs of x1 and all of its derivatives are the same (i.e., either all positive or all negative).  This is also true for x2 (though the signs for x1 may either be the same as or different from those for x2).  This can be a quick check for errors in your equations and/or free body diagrams.  (Note: if you choose the same positive directions for all variables, x1 and x2 will generally have opposite signs - this can be a quick check that your diagrams are correct).
  4. The only forces considered at each free body diagram are those that directly effect it.  For example, the forces at x2 include the position of x1 (through the sping k2) but don't include any of the other forces at x1.  For example, the applied for Fe doesn't appear in the free body diagram for x2; that is not to say that it doesn't affect x2, but the effect comes through the mathematical coupling of the equations.  (Note: If your are familiar with electrical circuits, this is similar to summing currents at a node).

Special Case 1: Input is a defined position (or velocity)

In the previous examples we used a free body diagram for each position in the diagram.  However, sometimes the input to the system is a position (for example if attached to a constant velocity motor).  In those cases, we don't need to include a free body diagram for that position.

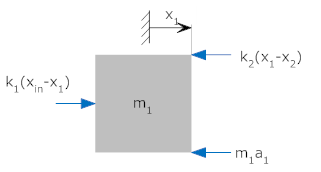
Example: Input defines one of the positions of the system

Consider the system below.  The leftmost position (xin) is an input to the system

 

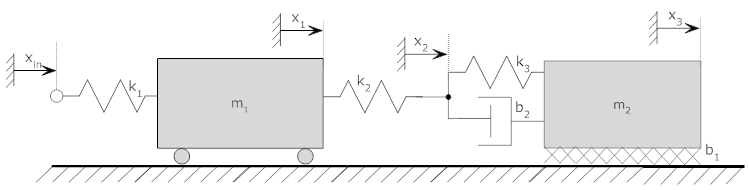
Even though there are four positions defined (xin, x1, x2 and x3) we only need to draw free body diagrams for three of them since xin is known (it is a defined input to the system).

Free body
diagram at x1
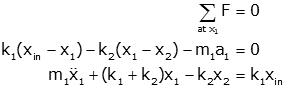Free body
diagram at x2		  
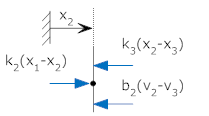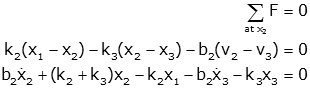Free body
diagram at x3


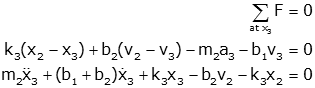Note that these free body diagrams and formulae obey the rules enumerated above.

Special Case 2: Gravity

So far we have always defined our displacements to be zero when springs are relaxed, neither compressed nor elongated.  There are many situations when other definitions of zero position are easier to work with.   For example, when gravity acts to extend (or compress) a spring, the gravitational force can be omitted from the analysis of system motion if the zero positions are taken when the system is at equilibrium with gravity.  This is best demonstrated with an example.

Example: The effect of gravity

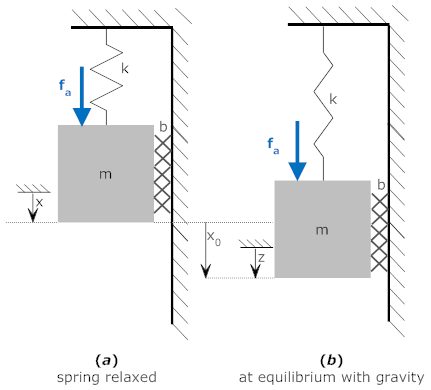
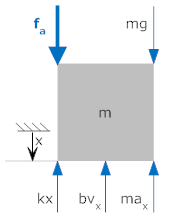
In figure (a), the position "x" is defined to be zero when the spring is in its relaxed position.  We can draw a free body diagram and find the equations of motion.  We draw the applied force, fa, and the force of gravity, m·g, to be downwards.  The forces k·x, b·vx and m·ax have their directions defined to be upward, i.e., opposite to the positive direction of x.  (Just to reiterate, this is not to say that the forces will be upward, just that we define them to be positive in the upward direction when the displacement is positive in the downward directions).

 

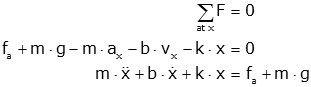When the system is at equilibrium and with no applied force, fa=0, the equation simplifies to

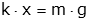
Let us call this distance x0.

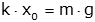
Now consider the situation shown in figure (b).  A new variable "z" is defined that is zero at the equilibrium position, z=x-x0, or x=z+x0.  If we plug this into the equations (and using the fact that the derivatives of x0 are all zero) we get

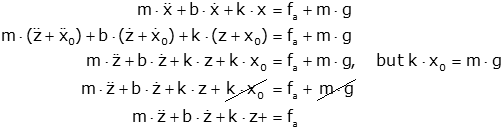
This last equation tells us that if we define our zero position to be when the system is at equilibrium with gravity, that we can ignore the effect of gravity.  This is a consequence of superposition.  We are essentially taking the two inputs (gravity and fa) and treating them separately.  Gravity gives a displacement of x0 from the position at which the spring is relaxed, and the displacement, z, is that due to the applied force.  We could not make this separation if the system was not linear.

 

In short, if we take figure (b) and define z=0 when the system is at equilibrium with gravity (and applied forces are zero), we can immediately draw a free body diagram and write the equations of motion without considering gravity.

 

   
Key Concept: Neglecting gravity  

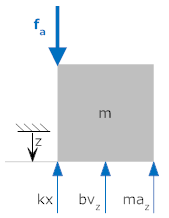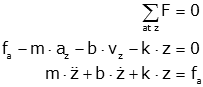If zero position is taken to be that at which the system is at equilibrium with gravity, then gravity can be ignored in the analysis.

Special Case 3: Relative Displacements

Often when making position measurements on a physical system, relative displacements are measured.  This can greatly simplify a physical measurement (e.g., measuring the relative distance between two objects may be easier than measureing both of their absolute positions).  However, it is important that D'Alembert's force (m·a) is measured relative to a fixed reference.  This is clarified in the following example.

Example: System Defined by Relative Displacements

In the system below a mass, m, is hung from a rectangular frame by a spring (k).  There is viscous friction between the frame and the mass on either side (b).  The distance xin positive upwards) is measured from a fixed reference and defines the position of the frame.  The distance z (measured downwards) is the position of the mass relative to the frame. 

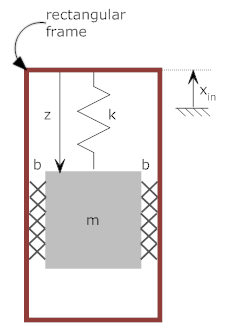
We will take the position, z, to be zero at equilibrium (so we need not consider gravity).   There are then four forces in the free body diagram:

  1. The force from the spring.  This is equal to k·z, upwards.
  2. The force from the friction on the left side of the mass.  This is equal to k·vz, upwards (vz is the first derivative of z with respect to time, i.e., the velocity).
  3. The force from the friction on the right side; this is also equal to  k·vz.
  4. D'Alembert's force which must use the acceration of the mass relative to a fixed reference.  The position of the mass relative to a fixed reference is xin-z. The D'Alembert forc will be upward (because z is defined positive downward) with a magnitude definced as

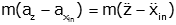
These are shown below, along with the resulting equations of motion.


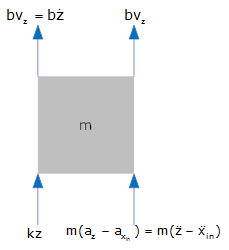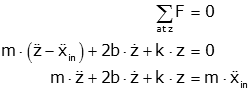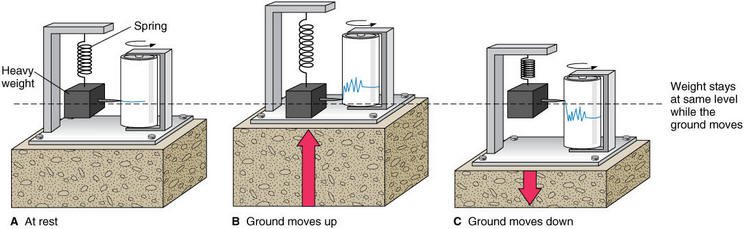
If anything in this discussion was unclear, refer to the same problem reworked without using relative displacements.  It may be useful to examine them side by side.

Note: This configuration is used in seismographs; the frame sits on the ground (so xin is the position of the ground) and the distance between the mass m and the frame is recorded (for example, a pen between the mass and the frame records the postion z).  In the diagram below (ref) the friction is not shown (but is accounted for by energy losses in the spring, air friction, pen friciton...).   As the ground moves, the system is designed such that the position of the mass is relatively constant.  The pen records the relative displacement, z, between the spring and the paper).


From: Physical Geology by Plummer, Carlson and Hammersley, McGraw Hill, 2016, page 386

 

 

Series and Parallel Elements

In many cases springs or friction elements may be placed in series or in parallel with each other. 

Parallel Elements

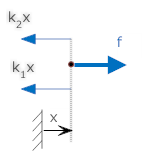
When two springs are placed in parallel (such that both springs have both ends in common), the effective spring constant adds.  The diagram below shows two springs in parallel, with the ends of the springs attached.  Also shown is a free body diagram, the resulting equations, and an equivalent spring.

Springs in parallel Free Body Diagram
                   
   
Equations Equivalent spring
              

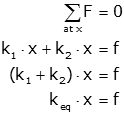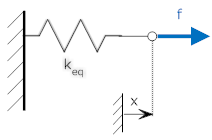Whenever there are two springs in parallel, they can be replaced by an equivalent spring whose spring constant is the sum of those of the parallel springs.  A similar statement can be made about friction elements.

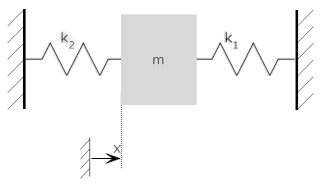
Note that it is not always so obvious that springs are in parallel.  Consider the example below.

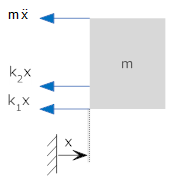
Springs in parallel Free Body Diagram
                   
   
Equations Equivalent spring
              

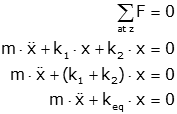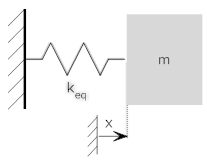Because the ends of the spring are in common; both have one end attached to the mass (displacement=x), and one end connected to a fixed reference (displacment=0).   An example of this that you have already seen is the seismograph, above - the friction elements are in parallel (one side is on the mass, and one on the frame) and so add in the free body diagram, and show up added in the equations of motion (as a "2b" term multiplied by the velocity).

Series Elements

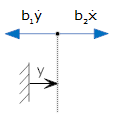
If two friction elements are in series, such that they have only one end in common, and nothing else is connected to that end, the inverse of the equivalent friction coefficient is equal to the sum of the inverses of the coefficients of the individual elements.  A similar statement holds for springs.  This is shown below.  Note: two free body diagrams are needed, because there are two unknown positions.  Note also that the position "x" is the displacement between the ends of the dashpot b2 ("x" is taken to be zero initially) - it is not measured relative to a fixed reference.

 Dashpots in Series Free Body Diagrams Equations

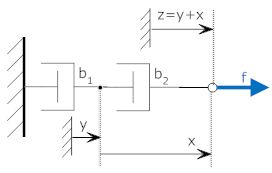The elongation of b2 is "x."
The rightmost end of b2 has displacement
"z" relative to a fixed reference.
          

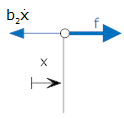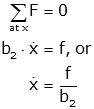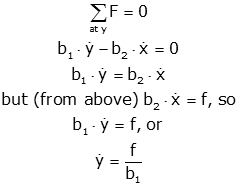Now we can draw the equivalent free body diagram and solve for the equivalent dashpot:

Free Body Diagram Equations
    

 

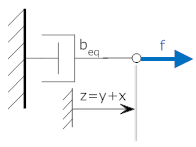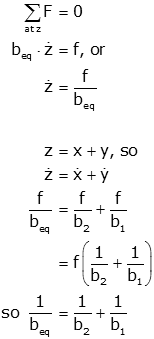The last equation is often rewritten directly for beq

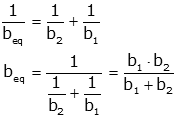
An example will show the utility of these concepts.

 

Example: Parallel and series elements

Consider the system below

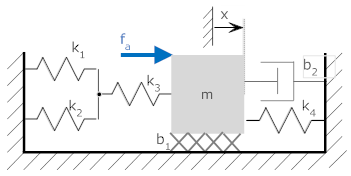k1 = 20 N/m
k2 = 10 N/m
k3 = 20 N/m
k4 = 15 N/m
b1 = 4 N-s/m
k2 = 3 N-s/m

We can make simplifications based on parallel and series elements

 



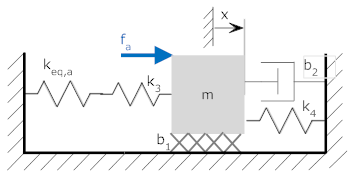 keq,a = k1 in parallel with k2
keq,a = k1 + k2 = 30 N/m
keq,a = 20 + 10 = 30 N/m


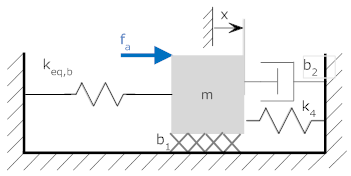keq,b = keq,a in series with k3
keq,b = keq,a·k3/(keq,a+k3)
keq,b = 30·20/(30+20) = 12 N/m


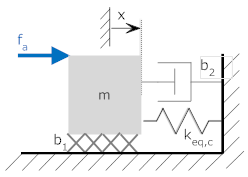keq,c = keq,b in parallel with k4
keq,c = keq,b + k4
keq,c = 12 + 15 = 27 N/m


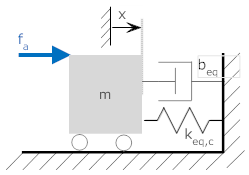beq = b1 in parallel with b2
beq = b1 + b2
beq = 3 + 4 = 7 N-s/m

(though not as obvious, one side of each friction element is on the mass, and the other is on the fixed reference).

So the resulting system is a simple mass-spring-dashpot system that is easily solved.

Note: Elements may not be connected in series if there is another element attached to their common endpoint.  For example, k1 and k2 may not be connected in the image below because the friction element, b, is also connected to their common point.

 

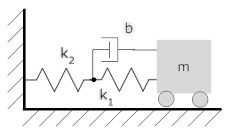
Key Concept: Parallel and Series elements

When two (or more) spring or friction elements are in parallel (i.e., such that both ends of the elements are connected), their values add.

When two (or more) spring or friction elements are in series (such that they have one end in common, with nothing else attached at that node), the inverse of the values add.

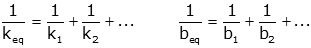
For only two elements in series

From System Diagram to State Space Model

It is possible to go directly from the system diagram to a state space model.  Details are here system diagram to a state space model.

Solving the model

Thus far we have only developed the differential equations that represent a system.  To solve the system, the model must be put into a more useful mathematical representation such as transfer function or state space.   Details about developing the mathematical representation are here.

References

© Copyright 2005 to 2019 Erik Cheever    This page may be freely used for educational purposes.

Erik Cheever       Department of Engineering         Swarthmore College