Laplace Transform Applied to Differential Equations and Convolution
Contents
The Laplace Transform has many applications. Two of the most important
are the solution of differential equations and convolution. These are
discussed below.
Differential Equations
The Laplace Transform can greatly simplify the solution of problems involving
differential equations.
Solving a first order differential equation
Consider the differential equation given by:
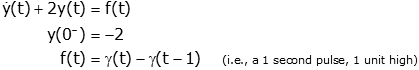
Find y(t).
Aside: Origin of the First Order Differential Equation
The differential equation with input f(t) and output y(t)
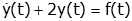
can represent many different systems. Two examples are given below,
one for a mechanical system and one for an electrical system.
Mechanical System
Input = force = φ(t). Output = velocity of mass. b=2, m=1.
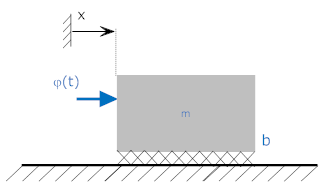
Free Body Diagram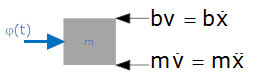
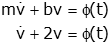
You can see that this is equivalent to the original equation (with output
v(t) and input φ(t)).
Electrical System
Input = current = ia(t). Output = voltage across
elements.
R=½, C=1.
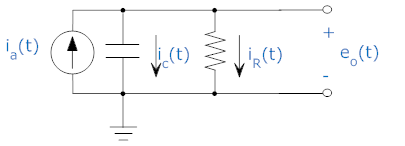
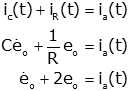
This is equivalent to the original equation (with output eo(t)
and input ia(t)).
Solution:
The solution is accomplished in four steps:
- Take the Laplace Transform of the differential equation. We
use the derivative property as
necessary (and in this case we also need the
time delay property)
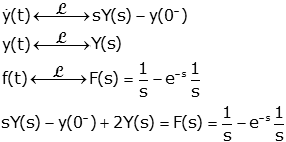
so
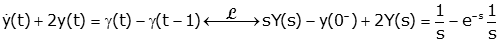
- Put initial conditions into the resulting equation
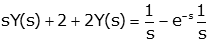
- Solve for Y(s)
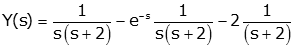
- Get result from the
Laplace Transform tables. (look up the terms
individually)
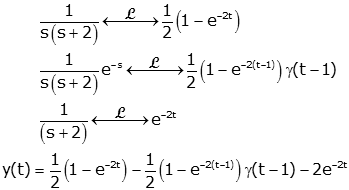
In this case all terms are in the
table and we need to apply the time
delay property. If the terms are not in the table, we need to
apply the methods of the
Inverse Laplace Transform. Note that the function is
implicitly zero for t<0. We could make this explicit by
multiplying by the unit step:
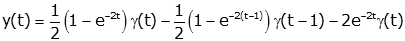
Key Concept: Using the Laplace Transform to Solve Differential Equations
The Laplace Transform can be used to solve differential equations using a
four step process.
- Take the Laplace Transform of the differential equation using the derivative property
(and, perhaps, others) as necessary.
- Put initial conditions into the resulting equation.
- Solve for the output variable.
- Get result from Laplace Transform
tables. If the result is in a form that is not in the tables,
you'll need to use the
Inverse Laplace Transform.
Solving a second order differential equation
Consider the differential equation given by:
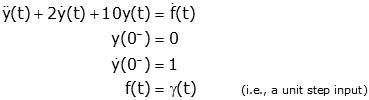
Find y(t).
Aside: Origin of the Second Order Differential Equation
Note: we could get such a second order differential equation by adding a
spring (k=10) between the mass and a fixed support, or an induction (L=1/10)
in parallel to the capacitor and inductor.
Solution:
Again, the solution can be accomplished in
four steps.
- Take the Laplace Transform of the differential equation using the derivative property
(and, perhaps, others) as necessary.
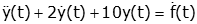
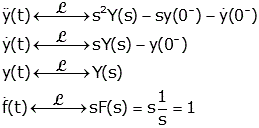
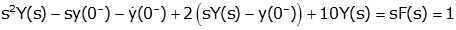
- Put initial conditions into the resulting equation.
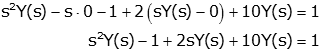
- Solve for the output variable.
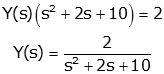
- Get result from Laplace Transform
tables. If the result is in a form that is not in the tables,
you'll need to use the
Inverse Laplace Transform. In this case, we can't factor the
denominator into real factors, (so we can't use the "double exponential"
form, but we can use the "generic decaying oscillatory"
form). By
completing the square we can rewrite the denominator
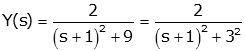
so
matching this with the "generic decaying oscillatory"
form we get B=0, C=2, a=1, ω0=3. We then use the table
to determine the solution
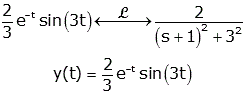
Again, the function is implicitly
zero for t<0.
Convolution
The convolution integral is very important in the study of systems. A
detailed description is available
here. In short, convolution can be used to calculate the zero state response (i.e., the response
to an input when the system has zero initial conditions) of a system to an arbitrary
input by using the impulse response of a system. Given a system impulse
response, h(t), and the input, f(t), the output, y(t) is the convolution of
h(t) and f(t):
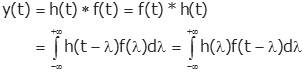
However, this integral can be quite hard to calculate in
this form, but is quite easy if using the Laplace Transform.
Example: Convolution in the Laplace Domain
Find y(t) given:
\[h\left( t \right) = e^{-t},\quad t\geq 0\]
\[f\left( t \right) = \left\{ {\begin{array}{*{20}{l}}
{0,}&{t < 0}&{(\sec tion\;1)} \\ {1,}&{0 \leq t \leq 2}&{(\sec tion\;2)} \\ {0,}&{2 < t}&{(\sec tion\;3)}
\end{array}} \right.\]
\[y(t) = f(t)*g(t)\] | f(t).svg) |
Note: This problem is solved
elsewhere in the
time domain (using the convolution integral). If you examine both techniques, you
can see that the Laplace domain solution is much easier.
Solution:
To evaluate the convolution integral we will use the convolution property of
the Laplace Transform:
\[y\left( t \right) = f\left( t \right) * h\left( t \right)\overset {\mathcal{L}} \longleftrightarrow Y\left( s \right) = F\left( s \right)H\left( s \right)\]
We need the Laplace Transforms of f(t) and h(t), but we can look them up in
the tables:
\[F(s) = \frac{1}{s} - {e^{ - 2s}}\frac{1}{s}\]
\[H(s) = \frac{1}{{s + 1}}\]
So
\[\eqalign{
Y(s) &= F(s)H(s) = \left( {\frac{1}{s} - {e^{ - 2s}}\frac{1}{s}} \right)\left( {\frac{1}{{s + 1}}} \right) \\
&= \frac{1}{{s\left( {s + 1} \right)}} - {e^{ - 2s}}\frac{1}{{s\left( {s + 1} \right)}}} \]
We can look up both of these terms in the
tables.
\[ \frac{1}{{s\left( {s + 1} \right)}}\overset {\mathcal{L}} \longleftrightarrow \left( {1 - {e^{ - t}}} \right)\gamma \left( t \right) \\
{e^{ - 2s}}\frac{1}{{s\left( {s + 1} \right)}}\overset {\mathcal{L}} \longleftrightarrow \left( {1 - {e^{ - \left( {t - 2} \right)}}} \right)\gamma \left( {t - 2} \right) \]
We can now write y(t) (which is implicitly zero for t<0, so I will drop the γ(t) term)
| \[y\left( t \right) = \left( {1 - {e^{ - t}}} \right) - \left( {1 - {e^{ - \left( {t - 2} \right)}}} \right)\gamma \left( {t - 2} \right)\] |  |
References
Replace
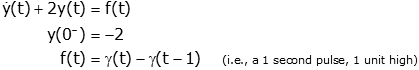
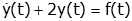


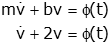

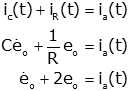
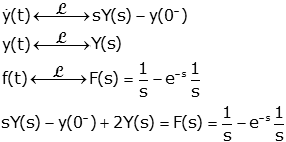
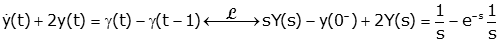
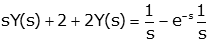
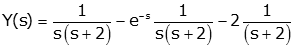
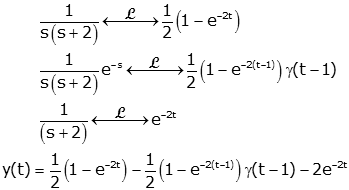
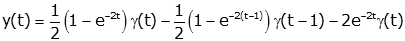
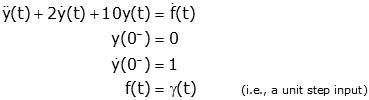
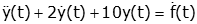
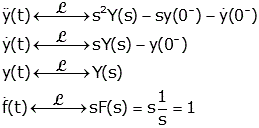
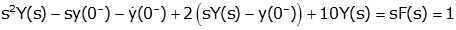
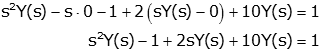
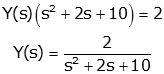
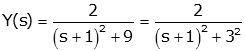
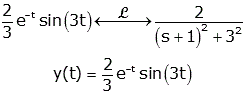
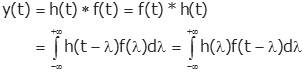
f(t).svg)
