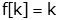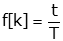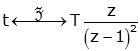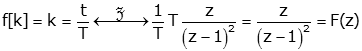| Entry |
Laplace Domain | Time Domain (Note)
All time domain functions are implicitly=0 for t<0 (i.e. they are multiplied by unit step). |
Z Domain (t=kT) |
|---|---|---|---|
| unit impulse | 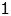 |
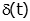 unit impulse unit impulse |
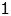 |
| unit step | 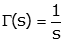 |
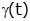 (Note) (Note)
u(t) is more commonly used to represent the step function, but u(t) is also used to represent other things. We choose gamma (γ(t)) to avoid confusion (and because in the Laplace domain (Γ(s)) it looks a little like a step input). |
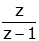 |
| ramp | 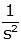 |
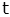 |
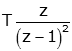 |
| parabola | 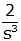 |
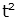 |
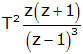 |
| tn (n is integer) |
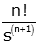 |
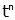 |
|
| exponential | 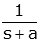 |
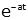 |
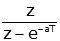 |
| power | 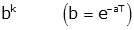 |
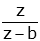 |
|
| time multiplied exponential |
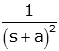 |
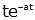 |
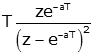 |
| Asymptotic exponential |
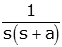 |
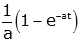 |
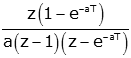 |
| double exponential |
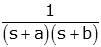 |
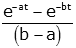 |
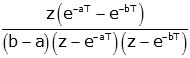 |
| asymptotic double exponential |
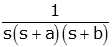 |
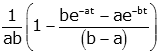 |
|
| asymptotic critically damped |
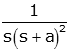 |
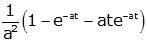 |
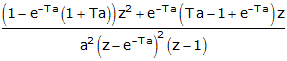 |
| differentiated critically damped |
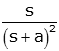 |
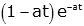 |
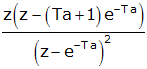 |
| sine | 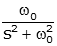 |
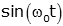 |
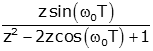 |
| cosine | 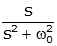 |
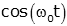 |
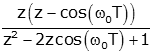 |
| decaying sine |
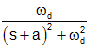 |
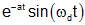 |
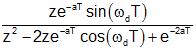 |
| decaying cosine |
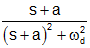 |
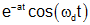 |
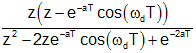 |
| generic decaying oscillatory |
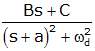 |
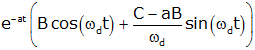 |
|
| generic decaying oscillatory (alternate) |
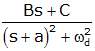 |
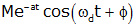 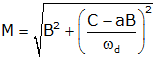 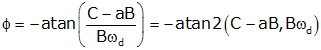 (Note) atan is the arctangent (tan-1) function. The atan function can give incorrect results (typically the function is written so that the result is always in quadrants I or IV). To ensure accuracy, use a function that corrects for this. In most programming languages the function is atan2. Also be careful about using degrees and radians as appropriate. |
|
| Z-domain generic decaying oscillatory |
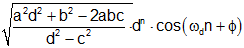 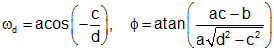 (Note) |
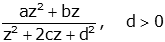 |
|
| Prototype Second Order System (ζ<1, underdampded) | |||
| Prototype 2nd order lowpass step response |
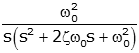 |
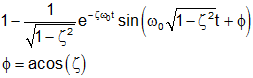 |
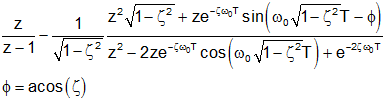 |
| Prototype 2nd order lowpass impulse response |
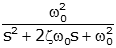 |
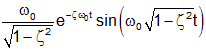 |
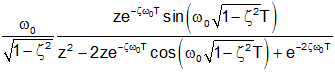 |
| Prototype 2nd order bandpass impulse response |
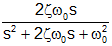 |
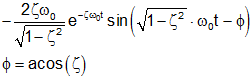 |
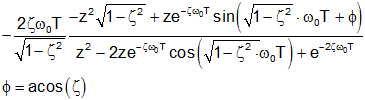 |