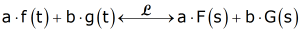
Contents
This section derives some useful properties of the Laplace Transform. These properties, along with the functions described on the previous page will enable us to us the Laplace Transform to solve differential equations and even to do higher level analysis of systems. In particular, the next page shows how the Laplace Transform can be used to solve differential equations. A table with all of the properties derived below is here.
The linearity property of the Laplace Transform states:
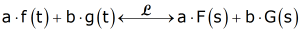
This is easily proven from the definition of the Laplace Transform
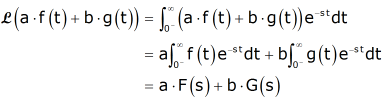
The time delay property is not much harder to prove, but there are some subtleties involved in understanding how to apply it. We'll start with the statement of the property, followed by the proof, and then followed by some examples. The time shift property states
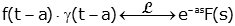
We again prove by going back to the original definition of the Laplace Transform
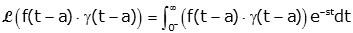
Because
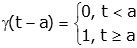
we can change the lower limit of the integral from 0- to a- and drop the step function (because it is always equal to one)
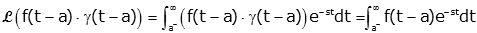
We can make a change of variable
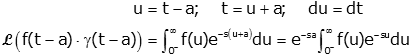
The last integral is just the definition of the Laplace Transform, so we have the time delay property
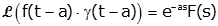
To properly apply the time delay property it is important that both the function and the step that multiplies it are both shifted by the same amount. As an example, consider the function f(t)=t·γ(t). If we delay by 2 seconds it we get (t-2)·γ(t-2), not (t-2)t·γ(t) or t·γ(t-2). All four of these function are shown below.
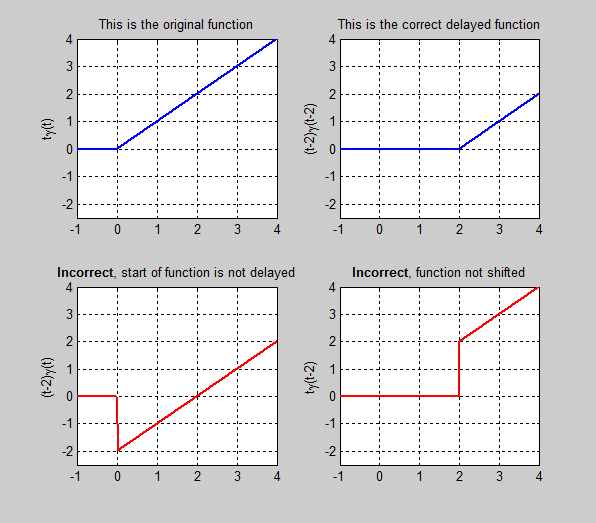
The correct one is exactly like the original function but shifted.
Important: To apply the time delay property you must multiply a delayed version of your function by a delayed step. If the original function is g(t)·γ(t), then the shifted function is g(t-td)·γ(t-td) where td is the time delay.
The first derivative property of the Laplace Transform states
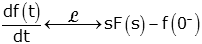
To prove this we start with the definition of the Laplace Transform and integrate by parts
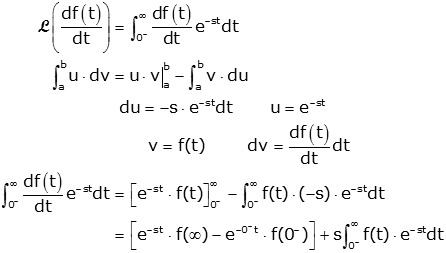
The first term in the brackets goes to zero (as long as f(t) doesn't grow faster than an exponential which was a condition for existence of the transform). In the next term, the exponential goes to one. The last term is simply the definition of the Laplace Transform multiplied by s. So the theorem is proved.
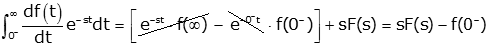
There are two significant things to note about this property:
Similarly for the second derivative we can show:
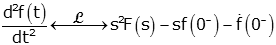
where
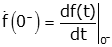
For the nth derivative:
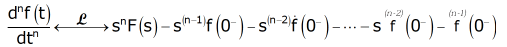
or
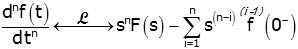
where
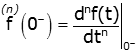
We will use the differentiation property widely. It is repeated below (for first, second and nth order derivatives)
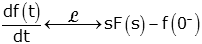
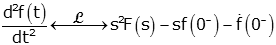
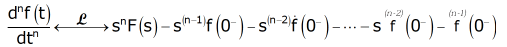
The integration theorem states that
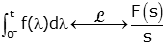
We prove it by starting by integration by parts
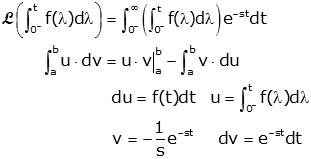
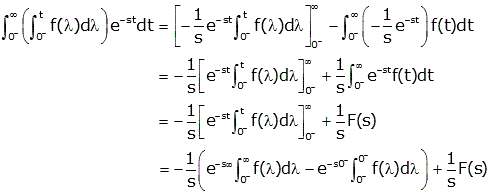
The first term in the parentheses goes to zero if f(t) grows more slowly than an exponential (one of our requirements for existence of the Laplace Transform), and the second term goes to zero because the limits on the integral are equal. So the theorem is proven
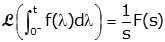
Given that the Laplace Transform of the impulse δ(t) is Δ(s)=1, find the Laplace Transform of the step and ramp.
Solution:
We know that
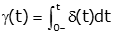
so that
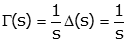
Likewise:
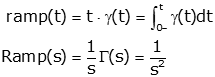
The convolution theorem states (if you haven't studied convolution, you can skip this theorem)
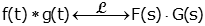
note: we assume both
f(t) and g(t) are
causal.
Causal functions are zero for t<0.
We start our proof with the definition of the Laplace Transform
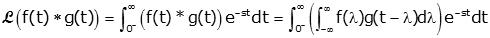
From there we continue:
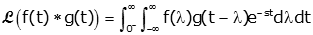 |
We can change the order of integration. |
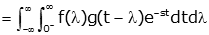 |
Now, we pull f(λ) out because it is constant with respect to the variable of integration, t |
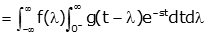 |
Now we make a change of variables |
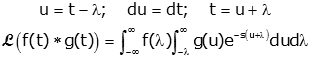 |
Since g(u) is zero for u<0, we can change the lower limit on the inner integral to 0-. |
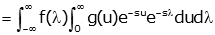 |
We can pull e-sλ out (it is constant with respect to integration). |
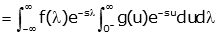 |
We can separate the integrals since the inner integral doesn't depend on λ. |
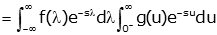 |
We can change the lower limit on the first integral since f(λ) is causal. |
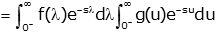 |
Finally we recognize that the two integrals are simply Laplace Transforms. |
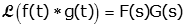 |
The Theorem is proven |
The initial value theorem states
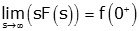
To show this, we first start with the Derivative Rule:
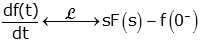
We then invoke the definition of the Laplace Transform, and split the integral into two parts:
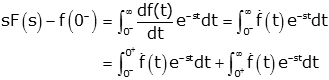
We take the limit as s→∞:
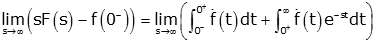
Several simplifications are in order. In the left hand expression, we can take the second term out of the limit, since it doesn't depend on 's.' In the right hand expression, we can take the first term out of the limit for the same reason, and if we substitute infinity for 's' in the second term, the exponential term goes to zero:
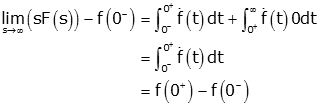
The two f(0-) terms cancel each other, and we are left with the Initial Value Theorem
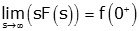
This theorem only works if F(s) is a strictly proper fraction in which the numerator polynomial is of lower order then the denominator polynomial. In other words is will work for F(s)=1/(s+1) but not F(s)=s/(s+1).
The final value theorem states that if a final value of a function exists that
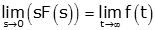
However, we can only use the final value if the value exists (function like sine, cosine and the ramp function don't have final values). To prove the final value theorem, we start as we did for the initial value theorem, with the Laplace Transform of the derivative,
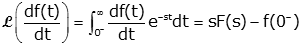
We let s→0,
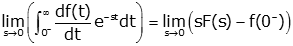
As s→0 the exponential term disappears from the integral. Also, we can take f(0-) out of the limit (since it doesn't depend on s)
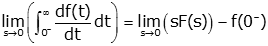
We can evaluate the integral
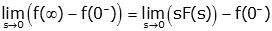
Neither term on the left depends on s, so we can remove the limit and simplify, resulting in the final value theorem
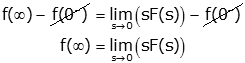
Examples of functions for which this theorem can't be used are increasing exponentials (like eat where a is a positive number) that go to infinity as t increases, and oscillating functions like sine and cosine that don't have a final value..
Some other properties that are important but not derived here are listed below.
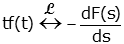
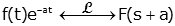
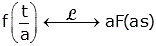
A table of properties is available here.