Use Fourier Xform Tables

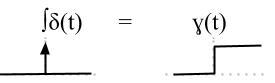
A short (2 page) table of Transform Pairs and Properties is available as Microsoft Word (.docx), pdf, or html (html is converted from Word, so it may be ugly).

Contents

Introduction

When faced with the task of finding the Fourier Transform (or Inverse) it can always be done using the synthesis and analysis equations.

$$\displaylines{
X(\omega ) = \int\limits_{ - \infty }^{ + \infty } {x(t){e^{ - j\omega t}}dt} \quad \quad {\rm{Analysis}} \cr
x(t) = {1 \over {2\pi }}\int\limits_{ - \infty }^{ + \infty } {X(\omega ){e^{j\omega t}}d\omega } \quad \quad {\rm{Synthesis}} \cr} $$

However, it is often possible to do so without these equations by using the Fourier Transofrm Pairs and Properties from a table (the examples below make use of the table with links at the very top of this page — it will be useful to have them easily accessible as you work through the solution).

Rather than explain the process conceptually, a series of illustrative examples are provided.

The Unit Impulse, x(t)=δ(t)

The Analysis Equation easily gives us X(ω)=1.

The Unit Step, x(t)=γ(t)

Use the Integral Property. Let us call y(t)=δ(t), so Y(ω)=1 (and Y(0)=1). In pictures

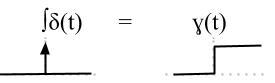
so

$$\displaylines{
x(t) = \int_{ - \infty }^t {\delta (\lambda )d\lambda } = \int_{ - \infty }^t {y(\lambda )d\lambda } \cr
X(\omega ) = {1 \over {j\omega }}Y(\omega ) + \pi Y(0)\delta (\omega ) = {1 \over {j\omega }} + \pi \delta (\omega ) \cr} $$

The Unit Pulse Function, x(t)=Π(t)

Use the Time Shift Property, Linearity and the result for the unit step, above. The unit pulse function is simply one time shifted step function, minus another shifted step function.

$$x(t) = \Pi (t) = \gamma \left( {t + {1 \over 2}} \right) - \gamma \left( {t - {1 \over 2}} \right)$$

In pictures we see that the pulse function is equal to a step (moved to the left by ½) minus another step (delayed by ½).

So the Fourier Transform pair is written as

$$x(t) = \gamma \left( {t + {1 \over 2}} \right) - \gamma \left( {t - {1 \over 2}} \right)\buildrel F \over
\longleftrightarrow \Gamma (\omega ){e^{ + j\omega {1 \over 2}}} - \Gamma (\omega ){e^{ - j\omega {1 \over 2}}} = X(\omega )$$

So

$$X(\omega ) = \left( {{1 \over {j\omega }} + \pi \delta (\omega )} \right){e^{ + j\omega {1 \over 2}}} - \left( {{1 \over {j\omega }} + \pi \delta (\omega )} \right){e^{ - j\omega {1 \over 2}}}$$

This clearly looks very different than the previous result, sinc(ω/2π), so let's massage the equation a little (and make use of the fact that δ(t)f(t)=δ(t)f(0), and Euler's identity for sine).

$$\eqalign{
X(\omega ) &= {1 \over {j\omega }}{e^{ + j\omega {1 \over 2}}} + \pi \delta (\omega ){e^{ + j\omega {1 \over 2}}} - {1 \over {j\omega }}{e^{ + j\omega {1 \over 2}}} - \pi \delta (\omega ){e^{ + j\omega {1 \over 2}}} \cr
&= {{{e^{ + j\omega {1 \over 2}}} - {e^{ + j\omega {1 \over 2}}}} \over {j\omega }} + \pi \delta (\omega ) - \pi \delta (\omega )\quad \quad \quad {\rm{Use}}\;\pi \delta (\omega ){e^{ + j\omega {1 \over 2}}} = \pi \delta (\omega ) \cr
&= {{{e^{ + j\omega {1 \over 2}}} - {e^{ + j\omega {1 \over 2}}}} \over {j\omega }} = {{2j\sin \left( {\omega {1 \over 2}} \right)} \over {j\omega }}\quad \quad \quad {\rm{Use}}\;{\rm{Euler's}}\;{\rm{identity}}\;{\rm{for}}\;{\rm{sine}} \cr
&= {{2\sin \left( {{\omega \over 2}} \right)} \over \omega } = {{\sin \left( {\pi {\omega \over {2\pi }}} \right)} \over {\pi {\omega \over {2\pi }}}} \cr
&= {\mathop{\rm sinc}\nolimits} \left( {{\omega \over {2\pi }}} \right) \cr} $$

which agrees with our previous result using the Analysis Equation (with Tp=1).

The Scaled Pulse Function, x(t)=Π(t/Tp)

Use the Time Scaling Property and the result for the unit pulse function, above.

$$\displaylines{ \Pi (t)\buildrel F \over
\longleftrightarrow {\mathop{\rm sinc}\nolimits} \left( {{\omega \over {2\pi }}} \right){\rm{,}}\quad \quad {\rm{so}} \cr
x(t) = \Pi \left( {{t \over {{T_p}}}} \right)\buildrel F \over
\longleftrightarrow {T_p}{\mathop{\rm sinc}\nolimits} \left( {{{\omega {T_p}} \over {2\pi }}} \right) = X(\omega ) \cr} $$

which agrees with our previous result using the Analysis Equation.

The Unit Pulse Function in ω, X(ω)=Π(ω)

Use Duality (the alternate form is easier in this case) along with the result for the Unit Pulse Function, above.

$$\Pi (t)\buildrel F \over
\longleftrightarrow {\mathop{\rm sinc}\nolimits} \left( {{\omega \over {2\pi }}} \right)$$

We replace the t by ω in Π(t) to get X(ω)=Π(ω) as our Fourier domain function. So we replace ω by -t in sinc(ω/2π) and divide by 2π to get x(t)=sinc(-ω/2π)/2π (we can remove the negative sign since sinc() is an even function)

$${1 \over {2\pi }}{\mathop{\rm sinc}\nolimits} \left( {{t \over {2\pi }}} \right)\buildrel F \over
\longleftrightarrow \Pi (\omega )$$

which agrees with our previous result using the Synthesis Equation (with Ωp=1).

The Unit Triangle Pulse, x(t)=Λ(t)

Use the convolution property since the Unit Triangle is simply the Unit Pulse Function convolved with itself: Λ(t)=Π(t)*Π(t).

$$\displaylines{
x(t) = \Pi (t) * \Pi (t)\buildrel F \over
\longleftrightarrow {\mathop{\rm sinc}\nolimits} \left( {{\omega \over {2\pi }}} \right) \cdot {\mathop{\rm sinc}\nolimits} \left( {{\omega \over {2\pi }}} \right) = X(\omega ) \cr
X(\omega ) = {{\mathop{\rm sinc}\nolimits} ^2}\left( {{\omega \over {2\pi }}} \right) \cr} $$

which agrees with our previous result using the Analysis Equation.

The Sawtooth

$$x(t) = sawtooth = \left\{ {\matrix{ {0,\quad t < 0,\;t > 1} \cr {t,\;\;\quad 0 \le t \le 1} \cr } } \right.$$

As an exercise, this Fourier Transform will be calculated in several different ways to demonstrate different applications of the tables to the same problem.

Method 1

The first method to be use is the analysis equation, though the integration is not shown here (it was previously done here).

$$X(\omega ) = {{{{\rm{e}}^{ - j\omega {\kern 1pt} }}{\mkern 1mu} {\kern 1pt} \left( {j\omega {\mkern 1mu} {\kern 1pt} + 1} \right) - 1} \over {{\omega ^2}}}$$

Method 2

We can represent the sawtooth as the integral of a shifted Unit Pulse function (to give the ramp) and a negative impulse (delayed by one second) to give the discontinuity at the end of the ramp (call this function y(t)=Π(t-½)-δ(t)).

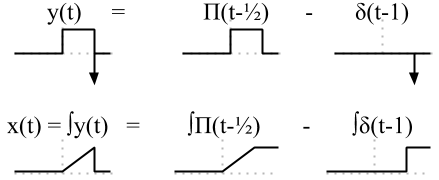
$$x(t) = \int\limits_{ - \infty }^t {\left( {\Pi \left( {\lambda - {1 \over 2}} \right) - \delta (\lambda - 1)} \right)} d\lambda = \int\limits_{ - \infty }^t {y(t)} d\lambda $$

We find Y(ω) by using the delay property and the transforms of the unit pulse and impulse.

$$\displaylines{ y(t) = \Pi \left( {t - {1 \over 2}} \right) - \delta \left( {t - 1} \right) \cr
Y(\omega ) = {\mathop{\rm sinc}\nolimits} \left( {{\omega \over {2\pi }}} \right){e^{ - {{j\omega } \over 2}}} - {e^{ - j\omega }} \cr} $$

We can now apply the integral property, with Y(0)=0, to find X(ω).

$$\eqalign{ X(\omega ) &= {{Y(\omega )} \over {j\omega }} - \pi Y(0)\delta (0) = {{Y(\omega )} \over {j\omega }} \cr
&= {{{\mathop{\rm sinc}\nolimits} \left( {{\omega \over {2\pi }}} \right){e^{ - {{j\omega } \over 2}}} - {e^{ - j\omega }}} \over {j\omega }} \cr} $$

This was much easier than the work required by "Method 1," but the result looks quite different. The result is correct in this form and no further work is required. However we perform this last step just to demonstrated that the two results are equivalent. Start by replacing sinc() with its definition (sinc(x)=sin(πx)/πx).

$$\eqalign{
X(\omega ) &= {{{\mathop{\rm sinc}\nolimits} \left( {{\omega \over {2\pi }}} \right){e^{ - {{j\omega } \over 2}}} - {e^{ - j\omega }}} \over {j\omega }} = {{{{\sin \left( {\pi {\omega \over {2\pi }}} \right)} \over {\pi {\omega \over {2\pi }}}}{e^{ - {{j\omega } \over 2}}} - {e^{ - j\omega }}} \over {j\omega }}\quad \quad \quad {\rm{substitute}}{\kern 1pt} \;{\rm{for}}\;{\mathop{\rm sinc}\nolimits} () \cr
&= {{2\sin \left( {{\omega \over 2}} \right)} \over {j{\omega ^2}}}{e^{ - {{j\omega } \over 2}}} - {{{e^{ - j\omega }}} \over {j\omega }}\quad \quad \quad {\rm{simplify}} \cr
&= {{2\left( {{{{e^{{{j\omega } \over 2}}} - {e^{ - {{j\omega } \over 2}}}} \over {2j}}} \right)} \over {j{\omega ^2}}}{e^{ - {{j\omega } \over 2}}} + {{j{e^{ - j\omega }}} \over \omega }\quad \quad \quad {\rm{Euler}}{\kern 1pt} \;{\rm{for}}\;{\rm{sin(),}}\;{\rm{bring}}\;{\rm{j}}\;{\rm{to}}\;{\rm{numerator}}\;{\rm{of}}\;{{\rm{2}}^{{\rm{nd}}}}\;{\rm{term}} \cr
&= {{\left( {{e^{{{j\omega } \over 2}}} - {e^{ - {{j\omega } \over 2}}}} \right)} \over {{j^2}{\omega ^2}}}{e^{ - {{j\omega } \over 2}}} + {{j{e^{ - j\omega }}} \over \omega } = - {{\left( {{e^{j0}} - {e^{ - j\omega }}} \right)} \over {{\omega ^2}}} + {{j{e^{ - j\omega }}} \over \omega }\quad \quad \quad {\rm{simplify}} \cr
&= {{{e^{ - j\omega }} - 1 + j\omega {e^{ - j\omega }}} \over {{\omega ^2}}} = {{{e^{ - j\omega }}(1 + j\omega ) - 1} \over {{\omega ^2}}}\quad \quad \quad {\rm{simplify, }}\;{\rm{common}}\;{\rm{denominator}} \cr} $$

As expected, the two methods have yielded equal results (but "Method 2" was easier and required only trivial multiplication).

Method 3

The sawtooth can also be created by a delayed pulse multiplied by time (and using the time multiplication property), x(t)=t·Π(t-½).

$${\rm{X(}}\omega {\rm{) = j}}{d \over {d\omega }}\left( {{\mathop{\rm sinc}\nolimits} \left( {{\omega \over {2\pi }}} \right){e^{ - {{j\omega } \over 2}}}} \right) = {{{{\rm{e}}^{ - j\omega {\kern 1pt} }} - 1 + j\omega {\mkern 1mu} {\kern 1pt} {{\rm{e}}^{ - j\omega {\kern 1pt} }}{\mkern 1mu} {\kern 1pt} } \over {{\omega ^2}}}$$

The derivative was calculated by a symbolic solver, and is clearly the same as before (it requires a somewhat difficult differentiation, and some algebra, but no integration) — it is not quite as easy as "Method 2," but shows that there are multiple ways to obtain the solution.

...Method n

There are a number of other methods. A class of methods that might seem like obvious choices involve multiplying equations in time, i.e., x(t)=Λ(t-1)·Π(t-½).

Though the representation in time is straightforward, there is a problem when we try to apply the rule in the frequency domain:

$$\displaylines{ \Lambda (t - 1)\buildrel F \over
\longleftrightarrow {{\mathop{\rm sinc}\nolimits} ^2}\left( {{\omega \over {2\pi }}} \right){e^{ - j\omega }} \cr
\Pi \left( {t - {1 \over 2}} \right)\buildrel F \over
\longleftrightarrow {\mathop{\rm sinc}\nolimits} \left( {{\omega \over {2\pi }}} \right){e^{ - {{j\omega } \over 2}}} \cr
\Lambda (t - 1) \cdot \Pi \left( {t - {1 \over 2}} \right)\buildrel F \over
\longleftrightarrow \left( {{{{\mathop{\rm sinc}\nolimits} }^2}\left( {{\omega \over {2\pi }}} \right){e^{ - j\omega }}} \right) * \left( {{\mathop{\rm sinc}\nolimits} \left( {{\omega \over {2\pi }}} \right){e^{ - {{j\omega } \over 2}}}} \right) \cr} $$

The resulting convolution (on the right of the arrow) is quite laborious, so this is not a good method. In general multiplication of two functions in the time domain is not a useful technique because of the resulting convolution in the frequency domain. Two exceptions to the rule are multiplication by time (used in "Method 3") because there is an entry in the table for time multiplication, and multiplication by a sine or cosine because it involves convolution with impulses. An example of the latter follows.

Windowed Sine Wave

Find the Fourier Transform of

$$\displaylines{ x(t) = \left\{ {\matrix{
{\sin ({\omega _0}t),\quad \quad |t| < {{6\pi } \over {{\omega _0}}} = {{{T_p}} \over 2}} \cr
{0,\quad \quad \quad \quad \quad \quad {\rm{otherwise}}} \cr } } \right. \cr
{\omega _0} = 2\pi ,\quad {T_p} = 6 \cr x(t) = \left\{ {\matrix{
{\sin (2\pi t),\quad \quad |t| < 3} \cr
{0,\quad \quad \quad {\rm{otherwise}}} \cr } } \right. \cr} $$		     

The windowed sine function is just the product of a sine wave and a rectangular pulse

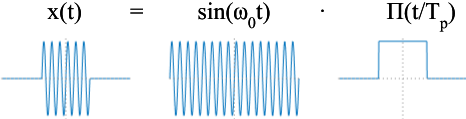
So the Fourier Transform is the convolution of the transforms of the sine and rectangular pulse in the frequency domain (divided by 2π). This is depicted below, followed by the required math.

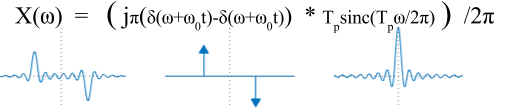
Note that the two leftmost graphs are of imaginary quantities (because of the multiplication by j).

$$\eqalign{
x(t) &= \sin ({\omega _0}t) \cdot \Pi \left( {{t \over {{T_p}}}} \right) \cr
X(\omega ) &= {1 \over {2\pi }}\left( {j\pi \left( {\delta (\omega + {\omega _0}) - \delta (\omega - {\omega _0})} \right)\; * \;\left( {{T_p}{\mathop{\rm sinc}\nolimits} \left( {{{{{\rm T}_p}\omega } \over {2\pi }}} \right)} \right)} \right) \cr
&= {j \over 2}\left( {\delta (\omega + {\omega _0}) * {T_p}{\mathop{\rm sinc}\nolimits} \left( {{{{{\rm T}_p}\omega } \over {2\pi }}} \right) - \delta (\omega - {\omega _0}) * {T_p}{\mathop{\rm sinc}\nolimits} \left( {{{{{\rm T}_p}\omega } \over {2\pi }}} \right)} \right) \cr
&= {j \over 2}\left( {{T_p}{\mathop{\rm sinc}\nolimits} \left( {{{{{\rm T}_p}(\omega + {\omega _0})} \over {2\pi }}} \right) - {T_p}{\mathop{\rm sinc}\nolimits} \left( {{{{{\rm T}_p}(\omega - {\omega _0})} \over {2\pi }}} \right)} \right)\quad \quad \quad \quad \quad \quad {\omega _0} = 2\pi ,\;{T_p} = 6 \cr
&= 3j\left( {{\mathop{\rm sinc}\nolimits} \left( {{{3(\omega - 2\pi )} \over \pi }} \right) - {\mathop{\rm sinc}\nolimits} \left( {{{3(\omega - 2\pi )} \over \pi }} \right)} \right) \cr} $$

Between the second and third step the fact that a function convolved with a shifted impulse gives a shifted version of the impulse, $f(x)*\delta(x-a)=f(x-a)$. This is an extremely important property of the impulse and is discussed here. The final result is shown below.

Key Concept: Using Fourier Transform Tables Instead of Synthesis/Analysis Equations

Tables of Fourier Transform Pairs and Properties can be quite useful for finding the Fourier Transform of a wide variety of functions. The trick is to figure out a combination of known functions and properties that will recreate the given function. Addition, time-shifting, integration, differentiation and convolution in time generally yield straightforward results. Multiplication in time is usually to be avoided except:

Tables

(this notice is also at the top of this page)
A short (2 page) table of Transform Pairs and Properties is available as Microsoft Word (.docx), pdf, or html (html is converted from Word, so it may be ugly).

Moving Forward

The last topic to be covered with respect to Fourier Transforms is using the Fourier Transform tables to calculate Fourier Series in most cases, obviating the need for the integrals in the Synthesis & Analysis equation.

 

References

Replace