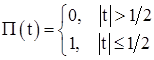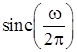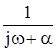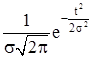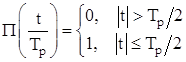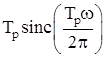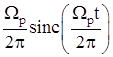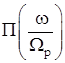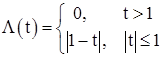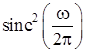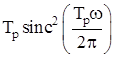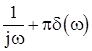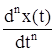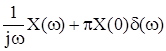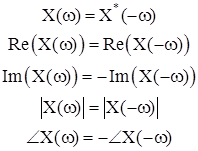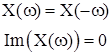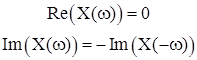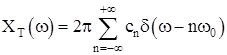Fourier Transform Pairs
More information at http://lpsa.swarthmore.edu/Fourier/Xforms/FXUseTables.html

Some Basic Functions

x(t)

X(ω)

(Synthesis)

(Analysis)

 
(impulse)


(constant)


(unit rectangular pulse, width=1)


(sinc)


(constant)


(impulse)


(complex exponential)


(shifted impulse)


(causal exponential)


(same as Laplace w/ s=jω)


(Gaussian)


(Gaussian)

Derived Functions (using basic functions and properties)

x(t)

X(ω)


(time scaled rectangular pulse, width=Tp)


(rectangular pulse in ω)


(triangular pulse, width=2)


(scaled triangular pulse, width=2Tp)

γ(t)
(unit step function)

Using these functions and some Fourier Transform Properties (next page), we can derive the Fourier Transform of many other functions.

Information at http://lpsa.swarthmore.edu/Fourier/Xforms/FXUseTables.html

© 2015, Erik Cheever

Fourier Transform Properties


Name

Time Domain

Frequency Domain

Linearity

Time Scaling

Time Delay (or advance)

Complex Shift

Time Reversal

Convolution

Multiplication

Differentiation

Integration

Time multiplication

Parseval’s Theorem

Duality

Symmetry Properties


x(t)

X(ω)

x(t) is real


Real part of X(ω) is even,
imaginary part is odd

x(t) real, even


X(ω) is real and even

x(t) real, odd


X(ω) is imaginary and odd

Relationship between Transform and Series


If xT(T) is the periodic extension of x(t) then:

Where cn are the Fourier Series coefficients of xT(t)
and X(ω) is the Fourier Transform of x(t)

Furthermore