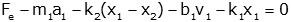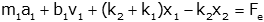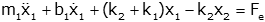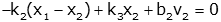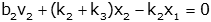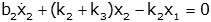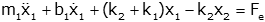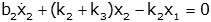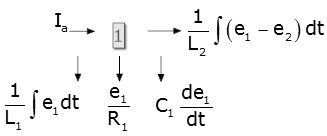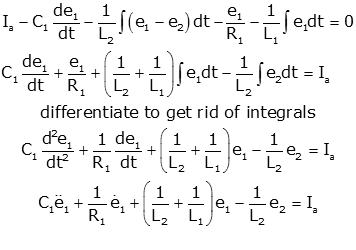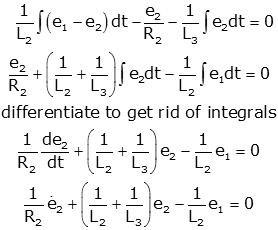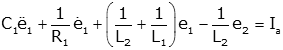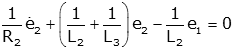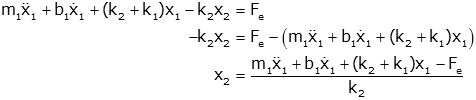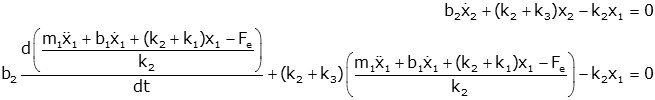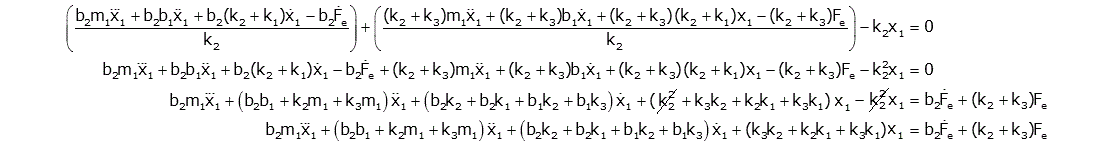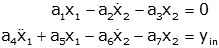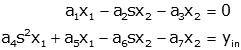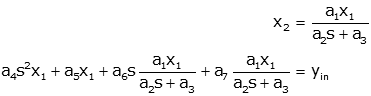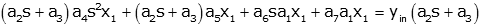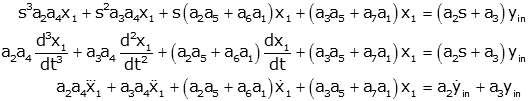When analyzing a physical system, the first task is generally to develop a mathematical description of the system in the form of differential equations. Typically a complex system will have several differential equations. The equations are said to be "coupled" if output variables (e.g., position or voltage) appear in more than one equation.
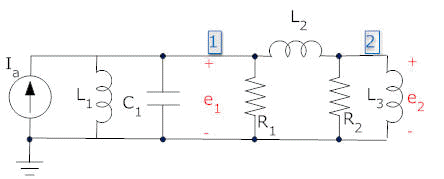
Two examples follow, one of a mechanical system, and one of an electrical system.
| System |
 |
|
| Free Body Diagrams |
 |
 |
| Coupled Differential Equations |    |
   |
The system is thus represented by two differential equations:
The equations are said to be coupled because x1 appears in both equation (as does x2).
| System |
 |
|
| Sum currents at nodes (note, each arrow shows direction of current into or out of node) |
 |
 |
| Coupled Differential Equations |  |
 |
The system is thus represented by two differential equations:
The equations are said to be coupled because e1 appears in both equation (as does e2).
Developing a set of coupled differential equations is typically only the first step in solving a problem with linear systems. The next step
A more useful form for describing a system is that of a single input-output differential equation. In such a description terms with the output and its derivatives goes on the left side of the equation, terms with the input and its derivatives goes on the right.
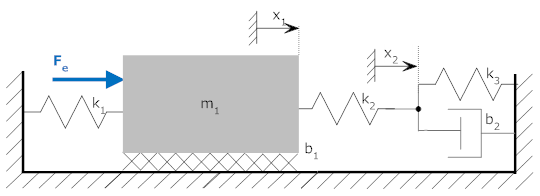
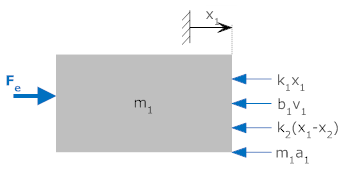
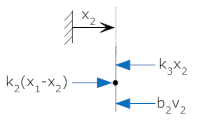
As an example consider the two coupled equations from the mechanical system above.
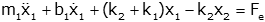
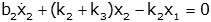
If we wish to solve for x1, we can simply solve the first equation for x2
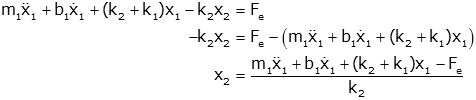
and put this expression into the second equation
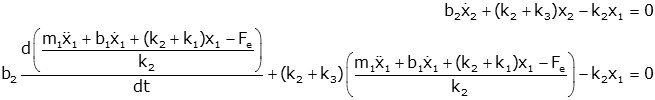
Simplifying, we get
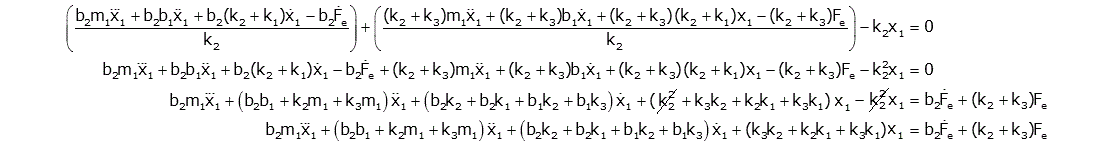
By convention the differential equation is written
Although this last expression is still very complicated, it is a single third order differential equation relating the output (x1) to the input (Fe). Using standard techniques, this equation can be solved in a straightforward manner.
Note: as expected all terms in front of x1 and its derivatives have the same sign. This is a general rule for passive (i.e., no motors, amplifiers...) systems.
It is often the case that a simple substitution, such as the one done above, is impossible. The next example demonstrates this.
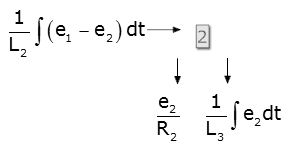
For example consider the case:
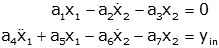
where the x1 and x2 are system variables, yin is an input and the an are all constants. In this case, if we want a single differential equation with s1 as output and yin as input, it is not clear how to proceed since we cannot easily solve for x2 (as we did in the previous example). What we can do in cases like this is to replace each derivative by a multiplication by a variable "s" (you'll see why this works when you study Laplace Transforms; for now, accept it without proof). We can solve the resulting algebraic equation, put it in terms of positive powers of "s." Each "s" in the final result is replaced by a derivative.
Let's apply the technique to this example. First replace derivatives by "s"
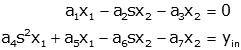
Now we can solve the first equation for x2 and put this into the second equation
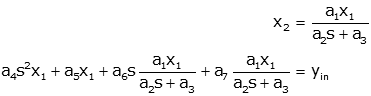
Multiply by a2s+a3 to get positive powers of s (no "s" terms in denominator).
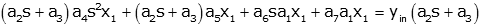
Now we collect like powers of s, and write the differential equation in descending order of derivative, with the output on the left and the input on the right.
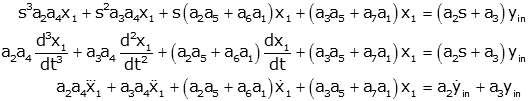
Since the differential equation is equivalent to the other mathematical representations of systems, there must be a way to transform from one representation to another. These methods are discussed here.