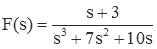
Partial fraction expansion (also called partial fraction decomposition) is performed whenever we want to represent a complicated fraction as a sum of simpler fractions. This occurs when working with the Laplace or Z-Transform in which we have methods of efficiently processing simpler fractions (If you are not yet familiar with these transforms, don't worry -- the technique also has other uses). Examples of partial fraction expansion applied to the inverse Laplace Transform are given here. The inverse Z Transform is discussed here.
As an example of partial fraction expansion, consider the fraction:
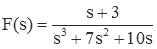
We can represent this as a sum of simple fractions:
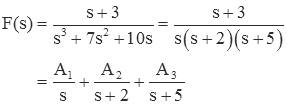
But how do we determine the values of A1, A2, and A3?
If we have a situation like the one shown above, there is a simple and straightforward method for determining the unknown coefficients A1, A2, and A3.
To find A1, multiply F(s) by s,
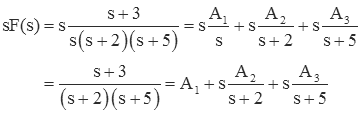
and then set s=0.
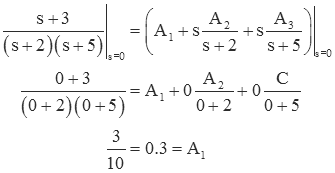
To find A2, multiply F(s) by s+2 and set s=-2.
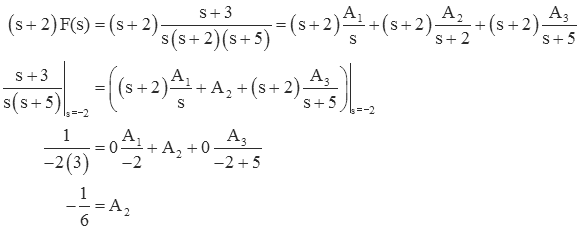
Likewise, for A3 multiply by s+5 and set s=-5
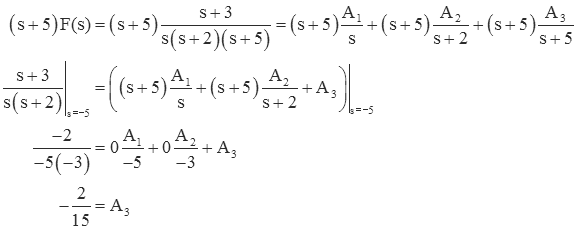
So, the final expansion is
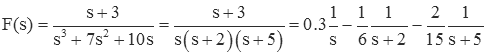
The result can be simply checked by putting all of the expanded terms over a common denominator.
The example given above shows that partial fraction expansion can easily expand a complex fraction into a sum of simpler fractions. However, there are many situations where the expansion is not so simple. The cases we will consider include
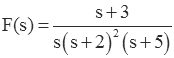
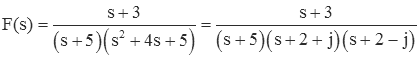
The partial fraction expansion methods described below can be used only when the order of the denominator polynomial is greater than that of the numerator.
The fraction
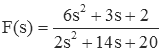
has numerator and denominator that are both second order. Before performing a partial fraction expansion, the fraction must be manipulated so that the order of the numerator is less than that of the denominator. A straightforward way to do this is to use long division on the fraction.
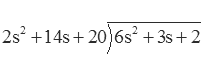
In order to get the s2 to drop out, multiply by 3.
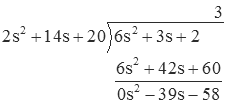
so the result is 3 with a remainder of -39s-58. Or, put another way
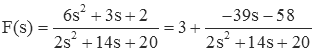
Partial fraction expansion can now be applied to the remaining fractional term of F(s).
Performing partial fraction expansions of an expression with distinct (i.e., not repeated) real roots. An example of this was done above. In general
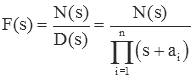
where the ai are all unique. In this expression D(s) is the denominator polynomial of order n, and N(s) is the numerator polynomial whose order is less than n. We want to perform a partial fraction expansion such that F(s) is expressed as:
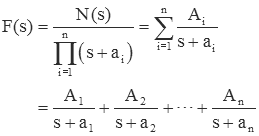
where
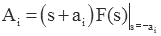
Consider the example from above:
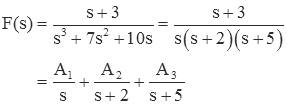
Find A1
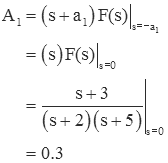
Find A2
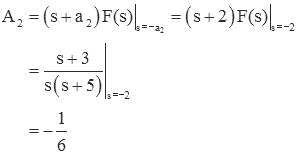
Find A3
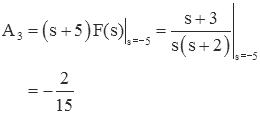
The calculation described above can, in practice, be very easily completed by hand by using the "cover-up" method.
Consider the example from above:
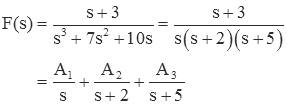
Find A1 by first "covering-up" the first term in the denominator (i.e., the term that is associated with A1) with your finger (shown as a gray ellipse), and then letting s=0.
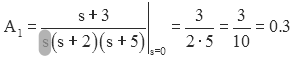
Likewise for A2
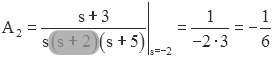
and A3
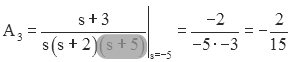
Situations in which there exists a repeated root in the denominator polynomial are more complicated. Consider the fraction:
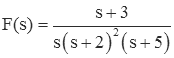
The expansion for this case is:
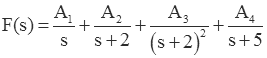
Most of the unknown coefficients can be found using the "cover-up" method.
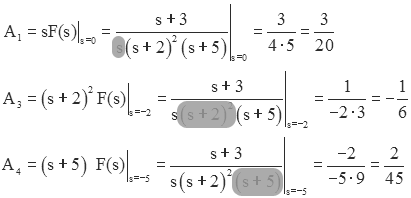
Unfortunately, the parameter A2 cannot be found in this way. Why not? {answer}
There are two commonly used methods for finding A2. The method favored by most textbooks uses the relationship
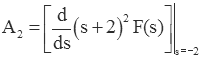
so
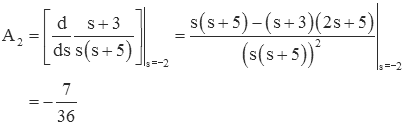
This yields,
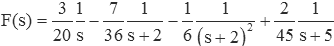
While this method is elegant (and can be extended to multiply repeated roots), the differentiation of the ratio of polynomials is prone to errors. This method won't be used again in this document {click for details of method}.
Another way to find the value of A2 that is completely general, involves no calculus, is useful in other situations, and can even be used to find the coefficients found by the cover-up method involves manipulation of the original equation describing the partial fraction expansion by performing a cross-multiplication.
Start with the partial fraction expansion
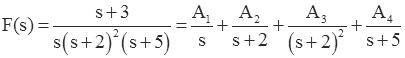
Multiply this by the denominator (to clear it out). In other words cross-multiply the right side by the denominator of the left side.
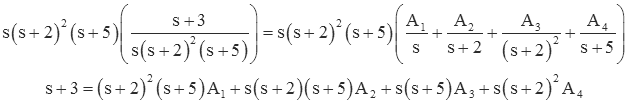
Now expand the right hand side as a polynomial in "s."
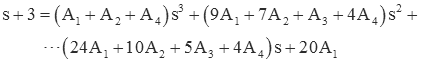
We are left with two polynomials that are equal to each other. We can use the fact that if two polynomials are equal, then the coefficient associated with each power in the polynomials must be equal. The polynomial on the left of the equals sign (i.e., s+3) only has 1st and 0th order terms, with values equal to 1 and 3, respectively. The right side is more complicated (as shown below).
| order of coefficient |
left side coefficient |
right side coefficient |
|---|---|---|
| 3rd (s3) | 0 | 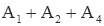 |
| 2nd (s2) | 0 | 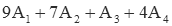 |
| 1st (s1) | 1 | 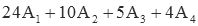 |
| 0th (s0) | 3 | 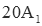 |
This yields a four-by-four system of equations that can be solved for A1 through A4.
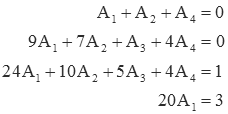
Or, expressed in matrix form

Solution yields:
A1 = 0.1500
A2 = -0.1944
A3 = -0.1667
A4 = 0.0444
Solution of a four-by-four system of equations is obviously more complicated than is the use of the cover-up method to find A1, A3 and A4, followed by using the differentiation method to find A2. This begs the question: why use the cross-multiplication technique? The answer is that the cross-multiplication technique need not be used in isolation. The cover-up method can be used to find A1, A3 and A4. Then the value of A2 can be found by using the expression (obtained using cross-multiplication)
A1+A2+A4=0,
or
A2=-(A1+A4)=-0.1944
Another case that often comes up is that of complex conjugate roots. Consider the fraction:
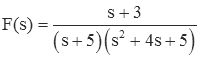
The second term in the denominator cannot be factored into real terms. This leaves us with two possibilities - either accept the complex roots, or find a way to include the second order term.
If we use complex roots, we can expand the fraction as we did before. This is not typically the way you want to proceed if you are working by hand, but may be easier for computer solutions (where complex numbers are handled as easily as real numbers). To perform the expansion, continue as before.
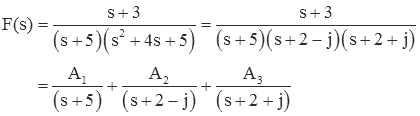
where
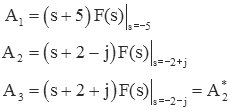
Note that A2 and A3 must be complex conjugates of each other since they are equivalent except for the sign on the imaginary part. Performing the required calculations:
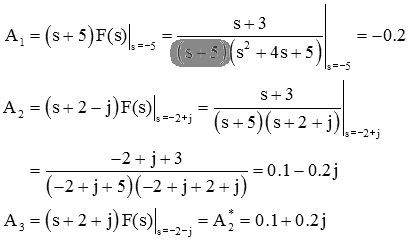
so
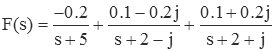
Another way to expand the fraction without resorting to complex numbers is to perform the expansion as follows.
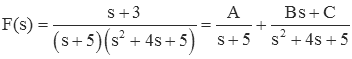
Note that the numerator of the second term is no longer a constant, but is instead a first order polynomial. From above (or using the cover-up method) we know that A=-0.2. We can find the quantities B and C from cross-multiplication.
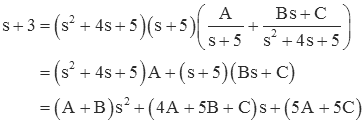
If we equate like powers of "s" we get
| order of coefficient |
left side coefficient |
right side coefficient |
|---|---|---|
| 2nd (s2) | 0 | A+B |
| 1st (s1) | 1 | 4A+5B+C |
| 0th (s0) | 3 | 5A+5C |
Since we already know that A=-0.2, the first expression (0=A+B) tells us that B=0.2, and the last expression (3=5A+5C) tells us that C=0.8. We can use the middle expression (1=4A+5B+C) to check our calculations. Finally, we get
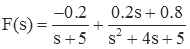
A situation that often confuses students is when there is an exponential term in the numerator. For example, the function
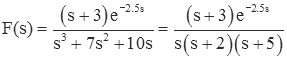
cannot be simplified to a form
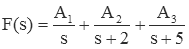
Instead, it is simplified to
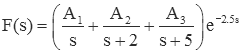
The quantities A1, A2 and A3 are found in the same way as for the case of distinct real roots (above). So
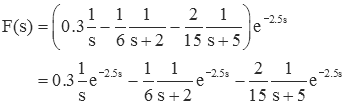
© Copyright 2005 to 2019 Erik Cheever This page may be freely used for educational purposes.
Erik Cheever Department of Engineering Swarthmore College