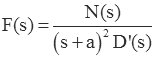
Consider the case in which one of the roots is repeated:
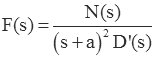
In this fraction the denominator polynomial has a repeated root at s=-a. The remainder of the denominator polynomial is called D'(s); it has no roots as s=-a. The numerator polynomial is N(s). If we expand this fraction we get
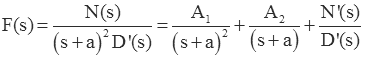
The term N'(s)/D'(s) represents the expansion of all of the terms except those with roots at s=-a.
We can find A1 by multiplying by (s+a)2 and setting s=-a (i.e., the cover-up method).
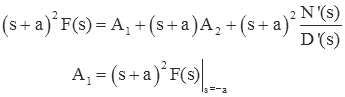
To find A2 we note that the we can get rid of the A1 term by differentiating the result above
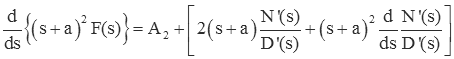
Now we can solve for A2 by setting s=-a.
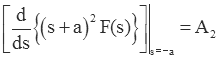
Now consider the case of multiply repeated roots (n>2).
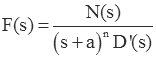
The resulting partial fraction expansion is
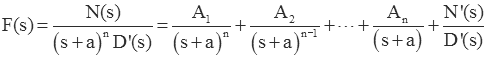
As before we can easily find A1 and A2
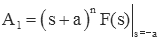
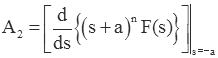
If we continue to differentiate we can find the other coefficients in a similar manner
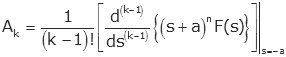
© Copyright 2005 to 2019 Erik Cheever This page may be freely used for educational purposes.
Erik Cheever Department of Engineering Swarthmore College