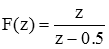
Given a Z domain function, there are several ways to perform an inverse Z Transform:
The only two of these that we will regularly use are direct computation and partial fraction expansion.
To understand how an inverse Z Transform can be obtained by long division, consider the function
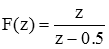
If we perform long division
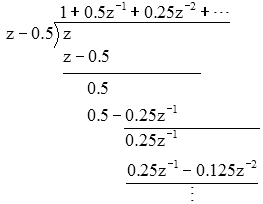
we can see that
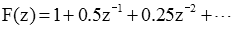 .
.
So the sequence f[k] is given by
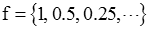
Upon inspection
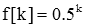
Note: We already knew this because the form of F(z) is one that we have worked with previously (i.e., the exponential function).
This technique is laborious to do by hand, but can be reduced to an algorithm that can be easily solved by computer.
The need for this technique, as well as its implementation, will be made clear when we consider transfer functions in the Z domain. We will present this method at that time.
This technique uses Partial Fraction Expansion to split up a complicated fraction into forms that are in the Z Transform table. If you are unfamiliar with partial fractions, here is an explanation.
As an example consider the function
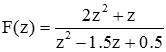
For reasons that will become obvious soon, we rewrite the fraction before expanding it by dividing the left side of the equation by "z."
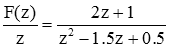
Now we can perform a partial fraction expansion
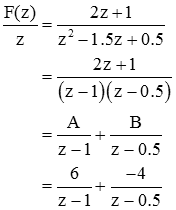
These fractions are not in our table of Z Transforms. However if we bring the "z" from the denominator of the left side of the equation into the numerator of the right side, we get forms that are in the table of Z Transforms; this is why we performed the first step of dividing the equation by "z."
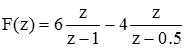
So
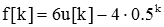
or
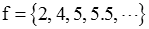
Verify the previous example by long division.
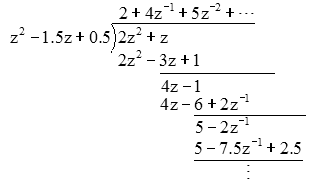
So
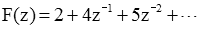
and the sequence f[k] is given by
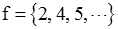
This method requires the techniques of contour integration over a complex plane. In particular
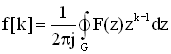 .
.
The contour, G, must be in the functions region of convergence. This technique makes use of Residue Theory and Complex Analysis and is beyond the scope of this document. Reference.
© Copyright 2005 to 2019 Erik Cheever This page may be freely used for educational purposes.
Erik Cheever Department of Engineering Swarthmore College