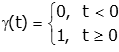
Contents
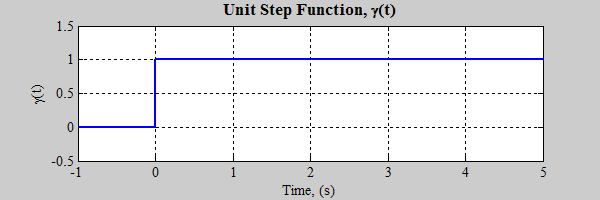
One of the most common test inputs used is the unit step function.
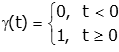

The step models many types of inputs: a switch turning on a voltage at t=0; a step change in road surface (e.g., a curb); a sudden change in temperature... The response of a system (with all initial conditions equal to zero at t=0-, i.e., a zero state response) to the unit step input is called the unit step response.
This page serves as a review of the method of finding the step response of first and second order system. It is assumed that the reader has studied this topic previously and merely needs a quick overview.
This section serves as a review of the calculation of the step response of first order systems by the method of homogeneous and particular (or natural and forced) response.
Consider the systems shown below. In the circuit the input and output are ein and eout, respectively. In the mechanical system the input and output are xin and xout, respectively. Find the unit step response of the sytstems. Remember, the unit step response is a zero state solution, so no energy is stored in the system at t=0- (i.e., the capacitor is discharged and the spring is uncompressed).
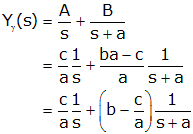
Solution:
First we need to find the
differential equation representing the systems. We do this by summing
currents at a node (eout) or forces (at
xout).
| Electrical Equations (sum of currents at eout) |
Mechanical Equations (sum of forces at xout) |
|
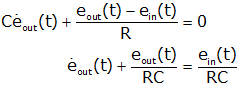 |
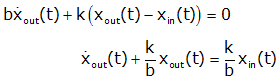 |
If we replace RC and k/b by τ, and set the input (ein(t) and xin(t)) to a unit step (γ(t)), and call the output "y" the equations become identical
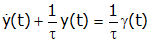
We now proceed with the solution:
We assume a homogeneous solution of the form
and put this into the differential equation (with the input set to 0) to get
where the coefficient A is yet to be determined.
We assume that the particular solution is a constant (since the input is constant for t>0).
The complete response is simply the sum of the homogeneous and particular responses.
We find "A" from initial conditions at t=0+. For the electrical circuit eout(0+)=0 (voltage across a capacitor cannot change instantaneously), and xout(0+)=0 (dashpot has finite force, hence finite velocity, hence continuous position: xout(0-)=xout(0+)).
The response is shown below for a τ=2 sec.
As a second example, consider the systems shown below in which we have swapped the components from the fires example. Find the unit step response of the systems. Remember, the unit step response is a zero state solution, so no energy is stored in the system at t=0- (i.e., the capacitor is discharged and the spring is uncompressed).
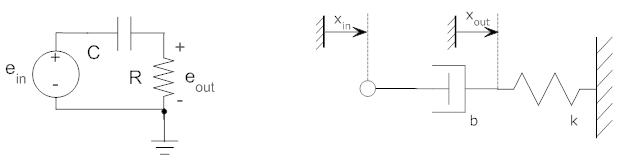
Solution:
First we need to find the
differential equation representing the systems. We do this by summing
currents at a node (eout) or forces (at
xout).
| Electrical Equations (sum of currents at eout) |
Mechanical Equations (sum of forces at xout) |
|
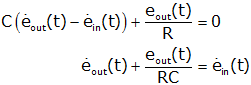 |
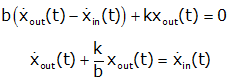 |
If we replace RC and k/b by τ, and set the input (ein(t) and xin(t)) to a unit step (γ(t)), and call the output "y" the equations become identical
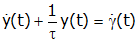
We now proceed with the solution:
We assume a homogeneous solution of the form
and put this into the differential equation (with the input set to 0) to get
where the coefficient A is yet to be determined.
We assume that the particular solution is a constant (since the input is constant for t>0).
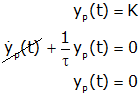
The complete response is simply the sum of the homogeneous and particular responses.
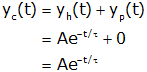
We find "A" from initial conditions at t=0+. For the electrical circuit eout(0+)=1 (voltage across a capacitor cannot change instantaneously, so eout(0+)=ein(0+)), and xout(0+)=1 (dashpot has finite force, hence finite velocity, hence cannot compress instantaneously: xout(0+)=xin(0+)).
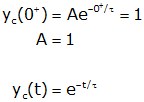
The response is shown below for a τ=2 sec.
A first order differential equation
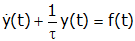
has homogeneous, particular, and complete responses given by
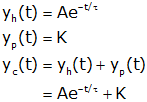
The unknown coefficient, "A," in the complete response is found from initial conditions at t=0+.
An easy way to remember unit step response of a first order system is:
\[{y_\gamma }\left( t \right) = {y_\gamma }\left( \infty \right) + \left( {y\left( {{0^ + }} \right) - {y_\gamma }\left( \infty \right)} \right){e^{ - t/\tau }}\]
This is depicted on the graph below. Note that the input starts at yγ(0+) and asymptotically approaches yγ(∞);
As you would expect, the response of a second order system is more complicated than that of a first order system. Whereas the step response of a first order system could be fully defined by a time constant and initial conditions, the step response of a second order system is, in general, much more complex. As a start, the generic form of a second differential equation that we might solve is iven by:
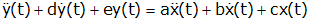
where y(t) is the output and x(t) is the input. We will proceed by examining a particular system.
To find the step response of a second order system like the one shown below
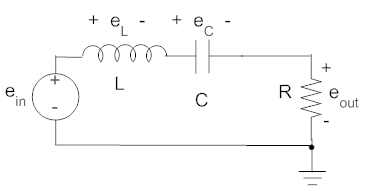
we start by finding the differential equation (using Kirchoff's voltage law) relating ein and eout.
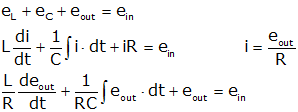
(differentiate to get rid of integral)
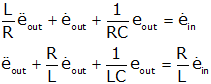
To find the homogeneous solution of a second order system, we proceed as before, i.e., we assume the form of the solution to be
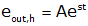
We set the input in the differential to zero, and substitute this expression and solve for "s."
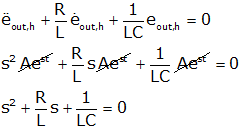
This last equation is called the "characteristic equation" of the system. Since we get a second order polynomial, we get two values for s
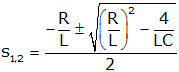
and our homogeneous solution becomes
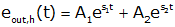
We now have two unknown coefficients, A1 and A2 to be determined from initial conditions. However we have three distinct cases that we will consider based upon the characteristics of s1 and s2. The simplest case occurs when s1 and s2 are real and negative and not equal to each other; we call this the overdamped case. If s1 and s2 are real and negative and equal to each other we call this the critically damped case. If s1 and s2 are complex conjugates (and have negative real parts), we say that the system is underdamped.
| Name | Roots of s | Characteristics of "s" |
| Overdamped | s=σ1, σ2 | Two real and negative roots |
| Critically Damped |
s=σ | A single negative real root |
| Underdamped | s=σ ± jωd | Complex conjugate with negative real part (j = √-1) |
It is also possible to have positive (or zero) real part - we will no first three cases are most important, and the last two will be discussed only briefly in what follows.
In the overdamped case we have two negative real roots at s1=σ1 and s2=σ2.
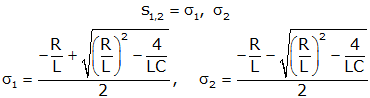
and
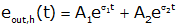
In the critically damped case, there is only a single negative root (i.e., the term under the square root sign is zero).
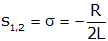
For this particular case, we have to adjust the form of the solution
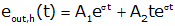
The last case we consider is the underdamped case (where we have two complex conjugate roots with negative real parts)
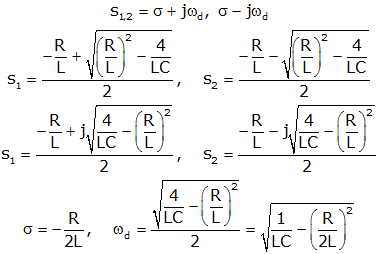
We can write the solution as
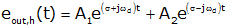
Since eout,h(t) is real A1 and A2 must be complex conjugates:
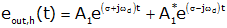
While this form of the homoegeneous response is correct, it can be shown that there are two forms that are equivalent
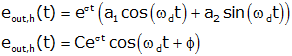
We will use the last expression.
If the input to a system is a step that is constant for t≥0, the particular response of the system is a constant.
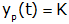
The complete response is simply the sum of the homogeneous and particular solutions. The unknown coefficients of the complete solution are found from initial conditions at t=0+ (because there are two unknown coefficients, two initial conditions are necessary).
Find the unit step response of the circuit shown (R=2, L=1, and C=1/5)

Solution:
We start by finding the differential
equation that defines the system:
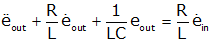
We then find the homogeneous response.
The characteristic equation is given by:
with roots at
This is the underdamped case with σ=-1 and ωd=2 so
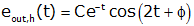
The particular response is just a constant, which we find by substituting into the equation (with t>0)
All derivatives are zero (because input and output are constant for t>0)
so
The complete response is the sum of the homogenous and particular solutions
The unknown coefficients are determined from initial conditions.
We know the current through the inductor doesn't change instantaneously, so the current through the circuit (and in particular, the resistor) is zero at t=0+.
We also know that the voltage across the capacitor doesn't change instantaneously, so all of the input voltage is across the inductor and
We use these two inital conditions to determine C and φ. First we apply the initial condition on the output voltage.
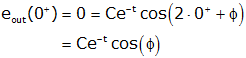
so φ is an odd multiple of π/2 radians (or 90°);. We will choose φ=pi/2. So
Next we apply the initial condition on the derivative of the output voltage (we employ the chain rule on the derivative of the right side of the equation)
and
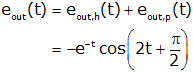
This is shown in the graph below
A second order differential equation
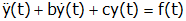
Has characteristic equation
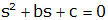
with roots at
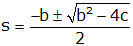
The characteristics of the roots determine the form of the
homogeneous response
| Name | Roots of s | Characteristics of "s" | Form of Homogeneous Response |
| Overdamped | s=σ1, σ2 | Two real and negative roots | 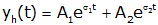 |
| Critically Damped |
s=σ | A single negative real root | 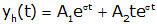 |
| Underdamped | s=σ ± jωd | Complex conjugate with negative real part (j = √-1) |
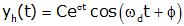 |
The particular response is given by
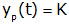
and the complete response is given by
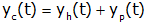
The complete response is simply the sum of the homogeneous and particular solutions. The unknown coefficients of the complete solution are found from initial conditions at t=0+ (because there are two unknown coefficients, two initial conditions are necessary).