Transfer Function → State Space (order of numerator=order of denominator)

• Controllable Canonical Form
• Observable Canonical Form

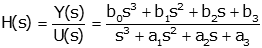
If the order of the numerator is equal to the order of the denominator, it becomes more difficult to convert from a system transfer function to a state space model.  This document shows how to do this for a 3rd order system.  The technique easily generalizes to higher order.

Controllable Canonical Form (CCF)

Consider the third order differential transfer function:

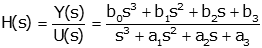
We start by multiplying by Z(s)/Z(s) and then solving for Y(s) and U(s) in terms of Z(s).  We also convert back to a differential equation.

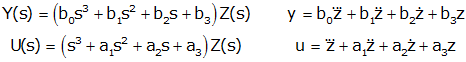
We can now choose z and its first two derivatives as our state variables

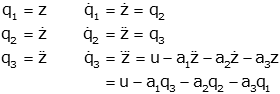
Now we just need to form the output

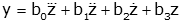
Unfortunately, the third derivative of z is not a state variable or an input, so this is not a valid output equation.  However, we can represent the term as a sum of state variables and outputs:

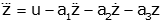
and

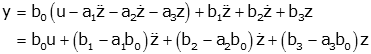
From these results we can easily form the state space model:

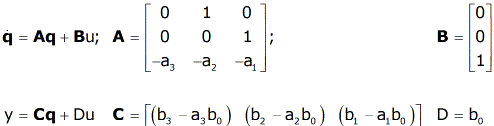
In this case, the order of the numerator of the transfer function was less than that of the denominator.  If they are equal, the process is somewhat more complex.  A result that works in all cases is given below; the details are here.

Observable Canonical Form (OCF)

Consider the third order differential transfer function:

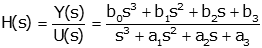
We can convert this to a differential equation and solve for the highest order derivative of y:

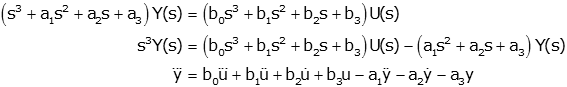
Now we integrate twice (the reason for this will be apparent soon), and collect terms according to order of the integral (this includes bringing the first derivative of u to the left hand side):

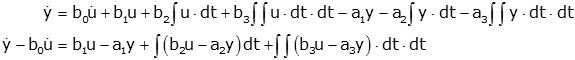
Without an justification we choose y-b₀u as our first state variable

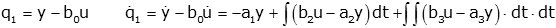
Looking at the right hand side of the differential equation we note that y=q₁ and we call the two integral terms q₂:

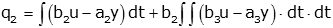
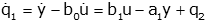
This isn't a valid state equation because it has "y" on the right side (recall that only state variables and inputs are allowed).  We can get rid of it by noting:

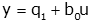
so

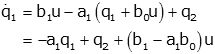
This is our first state variable equation. 

Now let's examine q₂ and its derivative:

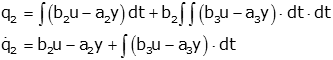
Again we note that y=q₁+b₀u and we call the integral terms q₃:

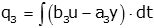
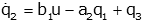
This is our second state variable equation. 

Now let's examine q₃ and its derivative:

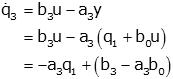
This is our third, and last, state variable equation.

Our state space model now becomes:

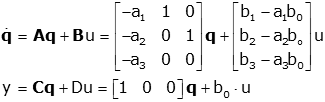
Here is a good reference that does the same derivations from a different perspective: http://www.ece.rutgers.edu/~gajic/psfiles/canonicalforms.pdf

References