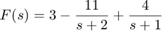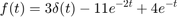Matlab for Laplace Transform Inversion / Partial Fraction Expansion

Contents

The code that generated this page is available at: http://lpsa.swarthmore.edu/LaplaceXform/InvLaplace/PFE1Matlab/PFE1.m

Background: Matlab and polynomials

Define the polynomial 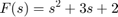$$F(s)=s^2+3s+2 $$

F=[1 3 2]

F =     1     3     2

Display it

poly2str(F,'s')

ans =   s^2 + 3 s + 2

Evaluate it as s=1

polyval(F,1)

ans =     6

Find roots, Note that since roots are at -1 and -2 the polynomial is (s+1)(s+2)

roots(F)

ans =
    -2
    -1

Define a second polynomial by its roots The polynomial is 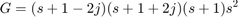$$ G=(s+1-2j)(s+1+2j)(s+1)s^2 $$

G=poly([-1+2j -1-2j -1 0 0]);
poly2str(G,'s')

ans =   s^5 + 3 s^4 + 7 s^3 + 5 s^2

Multiply polynomials H=FG (use convolution command)

H=conv(F,G)

H =     1     6    18    32    29    10     0     0

First Example - Simplest case - distinct real roots

To see this example worked out manually go to: http://lpsa.swarthmore.edu/LaplaceXform/InvLaplace/InvLaplaceXformPFE.html#Distinct_Real_Roots_

disp('Example 1: PFE with distinct real roots');

Example 1: PFE with distinct real roots

This case considers only distinct real roots.

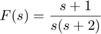
$$F(s)=\frac{s+1}{s(s+2)}$$

Define numerator and denominator polynomial.

n=[1 1];                %n=s+1
d=conv([1 0],[1 2]);    %Use "conv" to multiply polynomial
disp(['Numerator = ' poly2str(n,'s')]);
disp(['Denominator = ' poly2str(d,'s')]);

Numerator =    s + 1
Denominator =    s^2 + 2 s

Now use "residue" command to do inverse transform. r = magnitude of expansion term p = location of pole of each term k = constnat term (k=0 except when numerator and denominator are same order (m=n)).

[r,p,k]=residue(n,d)

r =
    0.5000
    0.5000
p =
    -2
     0
k =     []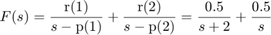

$$F(s)=\frac{\mathrm{r(1)}}{s-\mathrm{p(1)}} + \frac{\mathrm{r(2)}}{s-\mathrm{p(2)}} = \frac{0.5}{s+2} + \frac{0.5}{s} $$

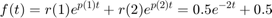
$$f(t)=r(1)e^{p(1)t} + r(2)e^{p(2)t} = 0.5e^{-2t} + 0.5$$

Note that the function is implicitly defined only for t>=0. Some texts show the time domain function multiplied by the unit step. We will keep our expressions simpler by making that relationship implicit.

Second Example - Repeated roots at origin

To see this example worked out manually go to: http://lpsa.swarthmore.edu/LaplaceXform/InvLaplace/InvLaplaceXformPFE.html#Repeated_Real_Roots_

disp('Example 2: PFE with repeated real roots (at origin in this case)');

Example 2: PFE with repeated real roots (at origin in this case)

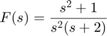
$$F(s)=\frac{s^2+1}{s^2(s+2)}$$

Define numerator and denominator polynomial.

n=[1 0 1];    %n=s^2+1
d=[1 2 0 0];  %d=s^2(s+2)=s^3+2s^2
disp(['Numerator = ' poly2str(n,'s')]);
disp(['Denominator = ' poly2str(d,'s')]);

[r,p,k]=residue(n,d)
Numerator =    s^2 + 1
Denominator =    s^3 + 2 s^2

r =
    1.2500
   -0.2500
    0.5000
p =
    -2
     0
     0
k =     []

Note, first order term (1/s) comes before the 2nd order term (1/s^2) in the Matlab results.

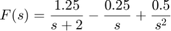
$$F(s)=\frac{1.25}{s+2} - \frac{0.25}{s} + \frac{0.5}{s^2}$$

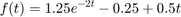
$$f(t)=1.25e^{-2t} - 0.25 +0.5t$$

Third Example - Complex Conjugate roots

To see this example worked out manually go to: http://lpsa.swarthmore.edu/LaplaceXform/InvLaplace/InvLaplaceXformPFE.html#ExampleRepeat

disp('Example 3: PFE with complex conjugate roots.');

Example 3: PFE with complex conjugate roots.

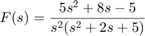
$$F(s)=\frac{5s^2 + 8s - 5}{s^2(s^2+2s+5)}$$

Define numerator and denominator polynomial.

n=[5 8 -5];     %n=s^2+1
d=[1 2 5 0 0];  %d=s^2(s^2+2s+5)=s^4+2s^3+5s^2
disp(['Numerator = ' poly2str(n,'s')]);
disp(['Denominator = ' poly2str(d,'s')]);

[r,p,k]=residue(n,d)
Numerator =    5 s^2 + 8 s - 5
Denominator =    s^4 + 2 s^3 + 5 s^2

r =
  -1.0000 - 1.0000i
  -1.0000 + 1.0000i
   2.0000 + 0.0000i
  -1.0000 + 0.0000i
p =
  -1.0000 + 2.0000i
  -1.0000 - 2.0000i
   0.0000 + 0.0000i
   0.0000 + 0.0000i
k =     []

Note, first two roots are complex conjugate roots.

Get magnitude and phase from magnitude and phase of pfe Refer to manual solution on web page listed above.

M=2*abs(r(1))       %Magnitude of cosine
phi=angle(r(1))     %Phase of cosine in radians

M =    2.8284
phi =   -2.3562

Get frequency and decay rate from location of pole

omega=abs(imag(p(1)))   % omega has to be positive
alpha=-real(p(1))
omega =     2
alpha =     1

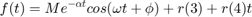
$$f(t)=Me^{-\alpha t}cos(\omega t+\phi) + r(3) + r(4)t$$

Plot the response

t=linspace(-1,4,1000);
f=(M*exp(-alpha*t).*cos(omega*t+phi) + r(3) + r(4)*t) .* heaviside(t);
plot(t,f,'Linewidth',2);
xlabel('Time'); ylabel('f(t)'); grid;

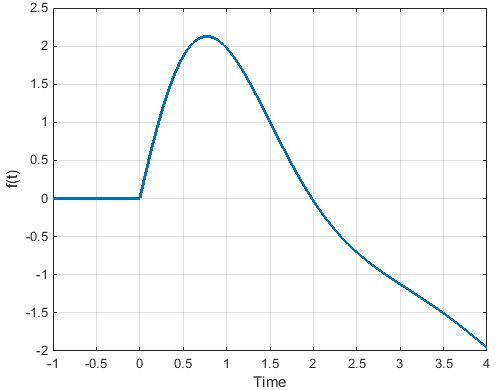
Fourth Example - Order of numerator=order of denominator

To see this example worked out manually go to: http://lpsa.swarthmore.edu/LaplaceXform/InvLaplace/InvLaplaceXformPFE.html#Order_of_numerator_polynomial_equals_order_of_denominator_

disp('Example 4: PFE: order of num=order of den');

Example 4: PFE: order of num=order of den

If the numerator and denominator have the same order, we get a constant as part of the partial fraction expansion.

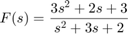
$$F(s)=\frac{3s^2 + 2s + 3}{s^2+ 3s + 2}$$

Define numerator and denominator polynomial.

n=[3 2 3];          %n=3s^2+2s + 3
d=[1 3 2];          %d=s^2+3s+2=(s+1)(s+2)
disp(['Numerator = ' poly2str(n,'s')]);
disp(['Denominator = ' poly2str(d,'s')]);

[r,p,k]=residue(n,d)
Numerator =    3 s^2 + 2 s + 3
Denominator =    s^2 + 3 s + 2

r =
   -11
     4
p =
    -2
    -1
k =     3

Note this time that k is not empty, k=3.

$$F(s)=3 - \frac{11}{s+2} + \frac{4}{s+1}$$

$$f(t)=3\delta (t) - 11e^{-2t} + 4 e^{-t}$$


Published with MATLAB® R2014b