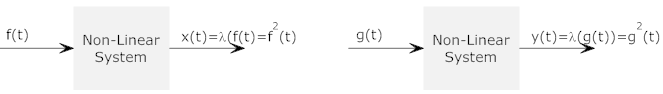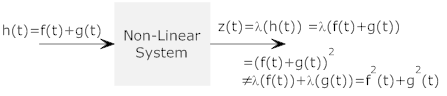Restrictions on Systems Studied

The systems considered by this page fall generally under the category of linear systems.  A lengthier description is "Linear, Time-Invariant, Continuous-Time, Continuous-Variable, Lumped-Parameter, Dynamic Systems."  Let's look at what these restrictive terms mean:

• Linear:  Essentially a linear system is one such that if you want to know the response of the system to an input h(t)=f(t)+g(t), you can simply find the response to f(t) and the response to g(t) and add them.
  • Example of a linear system:  Consider a system with input f(t) and output x(t).
                
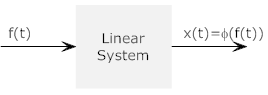
    Now if the input is changed to g(t) the output is y(t)
                
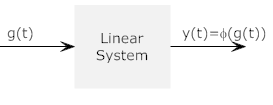
    If the system is linear, then an input of h(t)=g(t)+f(t) yields an ouput z(t)=x(t)+y(t)
         
    
    This result is important because it means that if we can express a complicated function like h(t) as the sum of simpler functions (e.g., f(t)+g(t)), we can simply solve the simpler problems and add the solutions
  • Example of a non-linear system:  Now consider the same situation when the system is nonlinear (for example a squaring function)
                
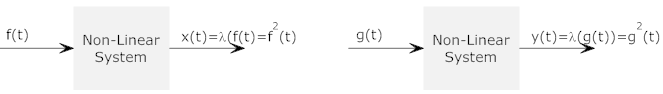
    Now we can no longer find the output to the complex function, h(t), by adding the responses of the system to the simpler function
         
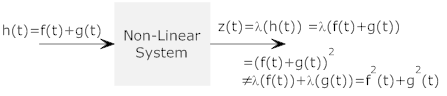
    Note the inequality in the last line.
  • Consequences of linearity:
    • If a system has several inputs, we can determine the output by simply summing the outputs to each input taken one at a time (superposition).  This is perhaps the most important property of linearity.
    • If we double the input (or multiply by any constant), the output is also doubled (or multiplied by the constant).
    • If the input to a system is sinusoidal, the output is sinusoidal at the same frequency; only the amplitude and/or phase may be changed.
• Time-Invariant:  For a time invariant system, the physical parameters of the system do not change with time.  The classic example of a non-time invariant system is a rocket whose mass changes with time (a time-invariant rocket would have constant mass).
• Continuous-Time:  Continuous time systems are what you are familiar with; time is a continuous, or real-valued, variable.  On the other hand discrete-time systems have time that moves in discrete steps.  Examples of discrete time systems include weekly closing stock prices (updated weekly), sound on a standard audio CD (updated 44,100 times per second).
• Continuous-Variable:  Again, most systems you are probably familiar with are continuous variable.  In these systems, variables are real-valued.  An example of a continuous variable system is a light on a dimmer switch - you can set the brightness to any value.  An example of a discrete-variable system would be a light with an on-off switch (only two possible values) or a dimmer with discrete detents so that the dimmer is forced to one of several values.
• Lumped-Parameter: A lumped parameter model treats the components of a system as a collection of discrete elements.  For example an inductor is normally treated as a discrete element with a single property (the inductance).  At high frequencies it might become important (especially at high frequencies) to consider how the voltage varies across the length of the inductance. This can be done by modeling the inductor as a infinite series of infinitesimally small inductors and resistors (a distributed-parameter system).  Another example is a tank of water.  For many analyses it is possible to use the average height of the water in the tank (lumped-parameter) to study behavior of the system, but sometimes it might be necessary to find a functional form for the height of the water in the tank as it sloshes about (distributed-parameter).
• Dynamic: A dynamic system is one that has an output that changes with time.  For example a circuit with capacitors, inductors and resistors and time varying inputs is dynamic.  A system with only resistors and constant sources is not considered a dynamic system.

While all of these restrictions seem to pigeonhole the subject matter quite a bit, many large and complex systems are understood in terms of linear systems.  We will on occasion consider systems that violate one or more of these restrictions.  We will generally study these violations as special cases, or extensions, of the topic of linear systems as presented in these pages.

References