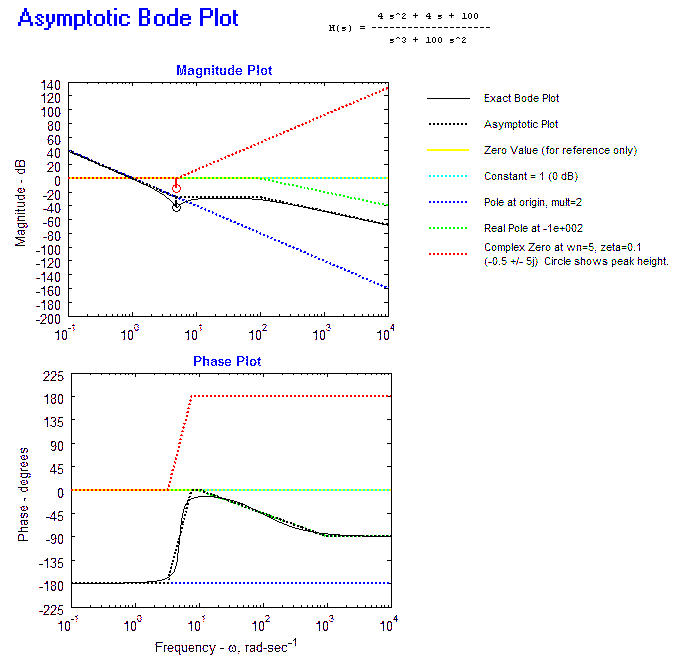
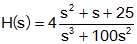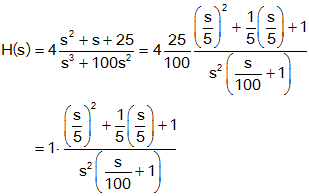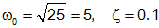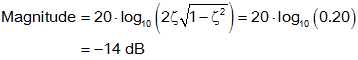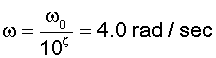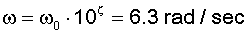Bode Plot: Example 6

Draw the Bode Diagram for the transfer function:

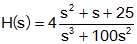
Step 1: Rewrite the transfer function in proper form.  

Make both the lowest order term in the numerator and denominator unity.  The numerator is an order 2 polynomial, the denominator is order 3.

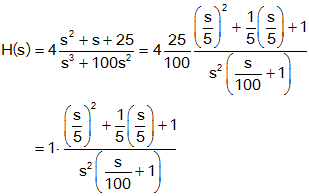
Step 2: Separate the transfer function into its constituent parts.

The transfer function has 4 components:

• A constant of 1
• A pole at s=-100
• A repeated pole at the origin (s=0)
• Complex conjugate zeros at the roots of s²+s+25, 
  with

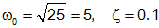
Step 3: Draw the Bode diagram for each part.

This is done in the diagram below.

• The constant is the cyan line (A quantity of 1 is equal to 0 dB).  The phase is constant at 0 degrees.
• The pole at 100 rad/sec is the green line.  It is 0 dB up to the break frequency, then falls with a slope of -20 dB/dec.  The phase is 0 degrees up to 1/10 the break frequency then falls linearly to -90 degrees at 10 times the break frequency.
• The repeated poles at the origin are shown with the blue line.  The slope is -40 dB/decade (because pole is repeated), and goes through 0 dB at 1 rad/sec.  The slope is -180 degrees (again because of double pole).
• The complex zero is shown by the red line.  The zeros give a dip in the magnitude plot of 
                
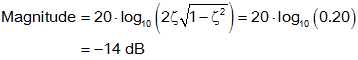
  at a frequency of 5 rad/sec (because ζ is small, ω_r≈ω₀).  This is shown by the red circle.  The phase goes from the low frequency asymptote (0 degrees) at
               
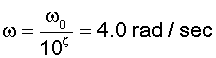
  to the high frequency asymptote at
               
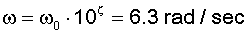
  Again, because ζ is so small, this line is close to vertical.

Step 4:  Draw the overall Bode diagram by adding up the results from step 3.

The exact response is the black line.