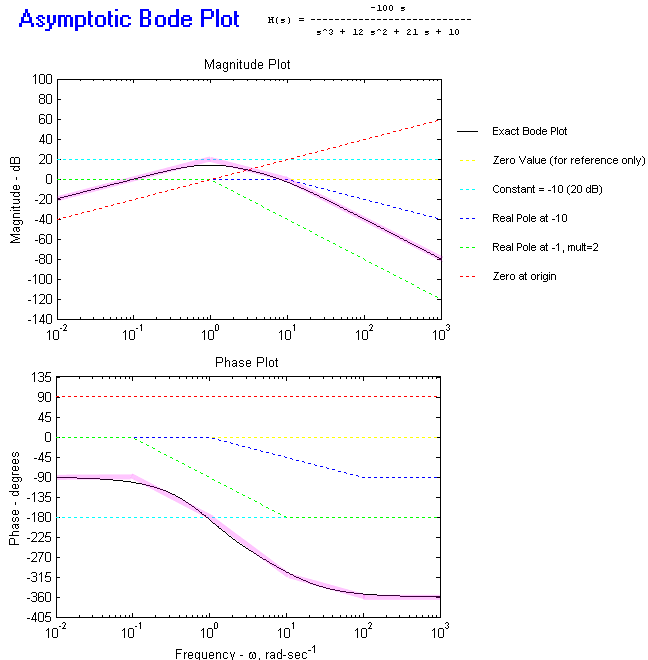
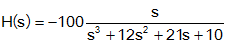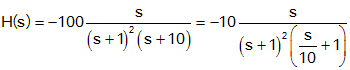Bode Plot: Example 4

Draw the Bode Diagram for the transfer function:

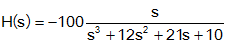
Step 1: Rewrite the transfer function in proper form.  

Make both the lowest order term in the numerator and denominator unity.  The numerator is an order 1 polynomial, the denominator is order 3.

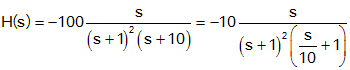
Step 2: Separate the transfer function into its constituent parts.

The transfer function has 4 components:

• A constant of -10
• A pole at s=-10
• A doubly repeated pole at s=-1 
• A zero at the origin

Step 3: Draw the Bode diagram for each part.

This is done in the diagram below.

• The constant is the cyan line (A quantity of 10 is equal to 20 dB).  The phase is constant at -180 degrees (constant is negative).
• The pole at 10 rad/sec is the blue line.  It is 0 dB up to the break frequency, then drops off with a slope of -20 dB/dec.  The phase is 0 degrees up to 1/10 the break frequency then drops linearly down to -90 degrees at 10 times the break frequency.
• The repeated pole at 1 rad/sec is the green line.  It is 0 dB up to the break frequency, then drops off with a slope of -40 dB/dec. The phase is 0 degrees up to 1/10 the break frequency then drops linearly down to -180 degrees at 10 times the break frequency.  The magnitude and phase drop twice as steeply as those for a single pole.
• The zero at the origin is the red line.  It has a slope of +20 dB/dec and goes through 0 dB at 1 rad/sec.  The phase is 90 degrees.

Step 4:  Draw the overall Bode diagram by adding up the results from step 3.

The overall asymptotic plot is the translucent pink line, the exact response is the black line.