The Derivative of Polynomial with Multiple Roots Equals Zero

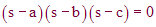
Consider a polynomial (we'll look only at third order case, but it easily generalizes) with distinct roots at a, b, and c:

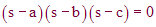
3rd order polynomial, distinct roots

Clearly this function is equal to zero at its roots (s=a, s=b, and s=c). But if we examine its derivative

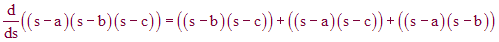derivative of polynomial, distinct roots ,

we find that it is not equal to zero at any of the roots.

Now consider a polynomial where the first root is a double root (i.e., it is repeated once):

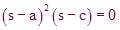
3rd order polynomial, repeated roots

This function is also equal to zero at its roots (s=a, s=b). If we examine its first derivative

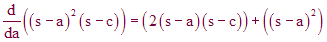
derivative of polynomial with repeated roots

we find that it is still equal to zero at the repeated root (s=a).

In general if we have a polynomial with a root repeated n times, its first n derivatives will be equal to zero.